Mathematics
Assertion (A): The length of the side of a regular hexagon is equal to the radius of its circumcircle.
Reason (R):
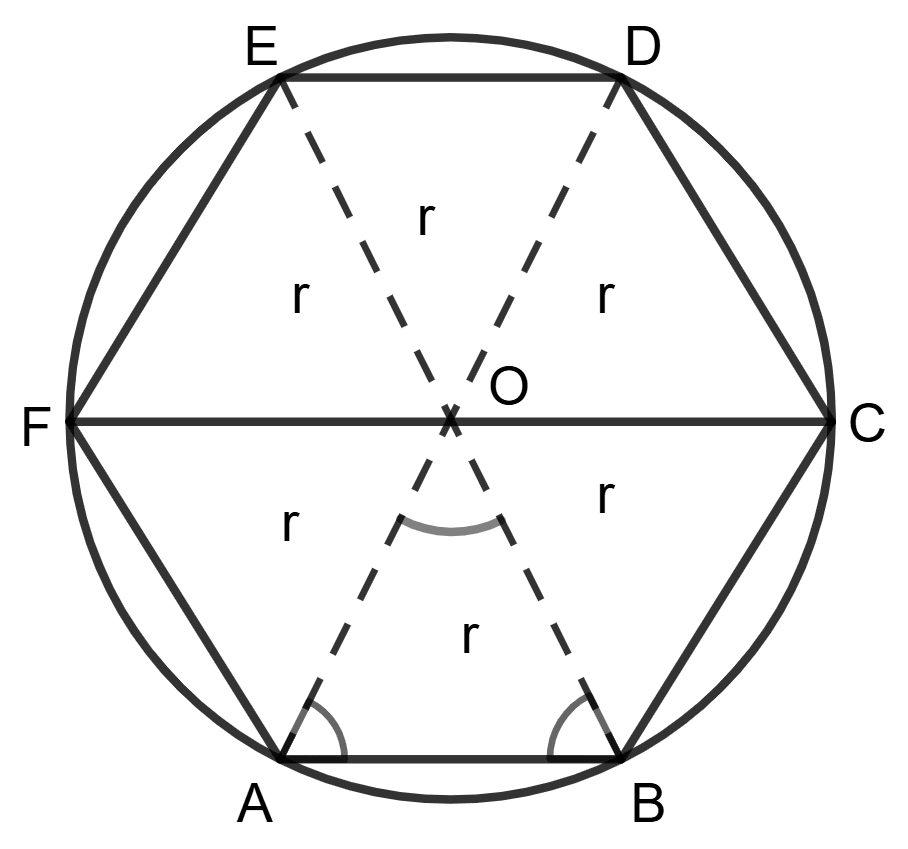
∠AOB =
∠OAB = ∠OBA =
⇒ OAB is an equilateral triangle
So, AB = OA = radius (r) of the circumcircle
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Rectilinear Figures
3 Likes
Answer
Both A and R are true.
Explanation
In a regular hexagon, all sides and angles are equal.
The circumcircle is the circle that passes through all six vertices of the hexagon. The center of the circumcircle is the same as the center of the hexagon.
A regular hexagon can be divided into six equilateral triangles by drawing lines from the center of the hexagon to its vertices. These lines are the radii of the circumcircle.
Each of these triangles is equilateral because the three sides of each triangle are the radius of the circumcircle (two sides) and the side of the hexagon (third side).
In a regular hexagon, the vertices are evenly spaced along the circle, ensuring all triangles are congruent and equilateral.
In an equilateral triangle, all three sides are equal. Thus, the length of the side of the hexagon is equal to the radius of the circumcircle.
∴ Assertion (A) is true.
∠ AOB = ∠ BOC = ∠ COD = ∠ DOE = ∠ EOF = ∠ FOA
So, ∠ AOB = = 60°
In Δ AOB,
AO = OB
⇒ ∠ OAB = ∠ OBA
Let ∠ OAB = x°
As we know that sum of all angles of triangle is 180°.
So, ∠ OAB + ∠ OBA + ∠ AOB = 180°
⇒ x° + x° + 60° = 180°
⇒ 2x° + 60° = 180°
⇒ 2x° = 180° - 60°
⇒ 2x° = 120°
⇒ x° =
⇒ x° = 60°
So, ∠ OAB = ∠ OBA = ∠ BOA = 60°
∴ AOB is a equilateral triangle.
∴ Reason (R) is true.
Hence, both Assertion (A) and Reason (R) are true.
Answered By
2 Likes
Related Questions
Assertion (A): ABCD is a parallelogram. AX is bisector of ∠A, CY is bisector of ∠C. Then quadrilateral AXCY is also a parallelogram.
Reason (R): If any one pair of opposite sides of a quadrilateral are equal and parallel then the quadrilateral is a parallelogram.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): In the given figure, if the area of the parallelogram ABEF is 120 cm2, then area of rectangle ABCD is 120 cm2.
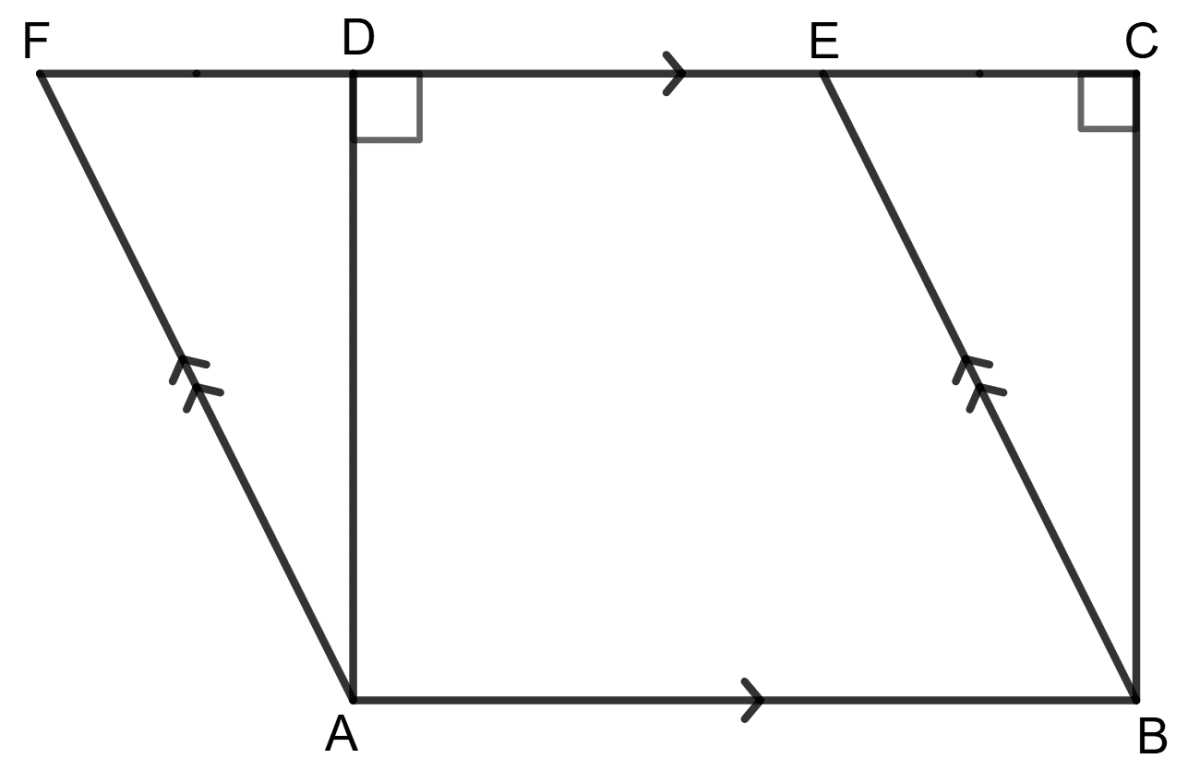
Reason (R): Parallelogram and rectangle on the same base and between the same parallels are equal in area.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Rhombus becomes square if its diagonals are equal.
Reason (R): OB = OD =
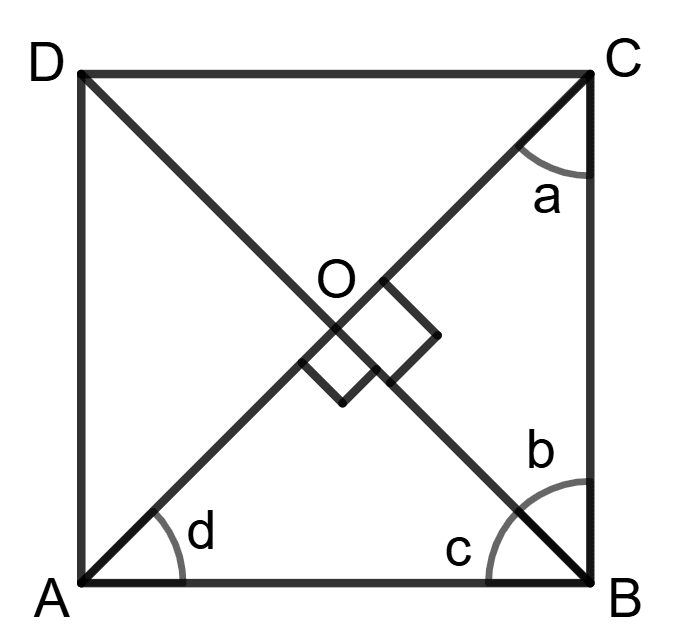
and OC = OA =
⇒ OB = OA = OC
OB = OC
⇒ ∠a = ∠b = 45°
Similarly, ∠c = ∠d = 45°
∠ABC = ∠b + ∠c = 45° + 45° = 90°- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): In the given figure, square ABCD and △APB are equal in area.
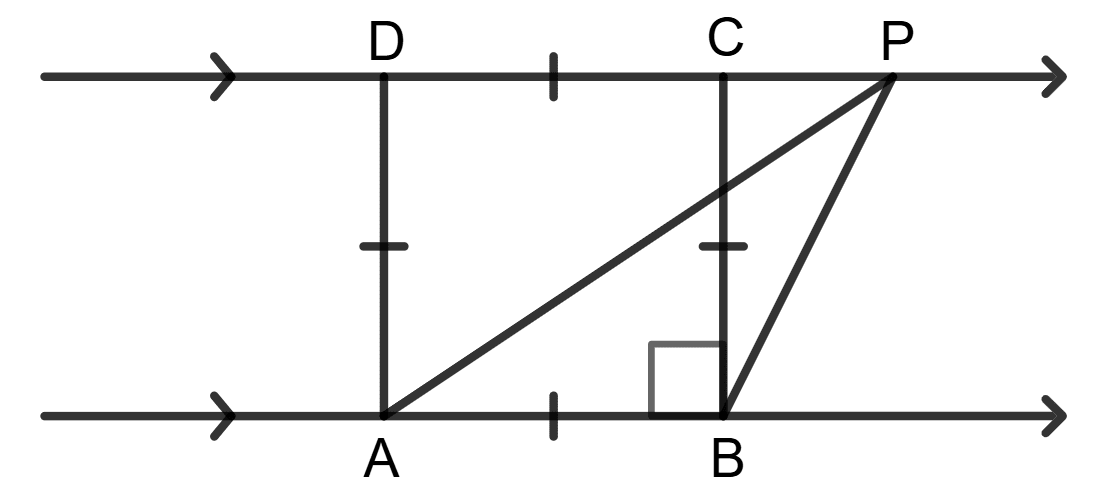
Reason (R): Square ABCD and △APB are on the same base (AB) and between the same parallels (AB//DP).
⇒ Area of △APB =
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.