Mathematics
Assertion (A): The line segment joining the mid-points of all parallel chords of a circle passes through the centre.
Reason (R): If the chords are on same side of centre then only the line through the mid-points of the chords passes through the centre.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Circles
1 Like
Answer
A is true, R is false.
Explanation
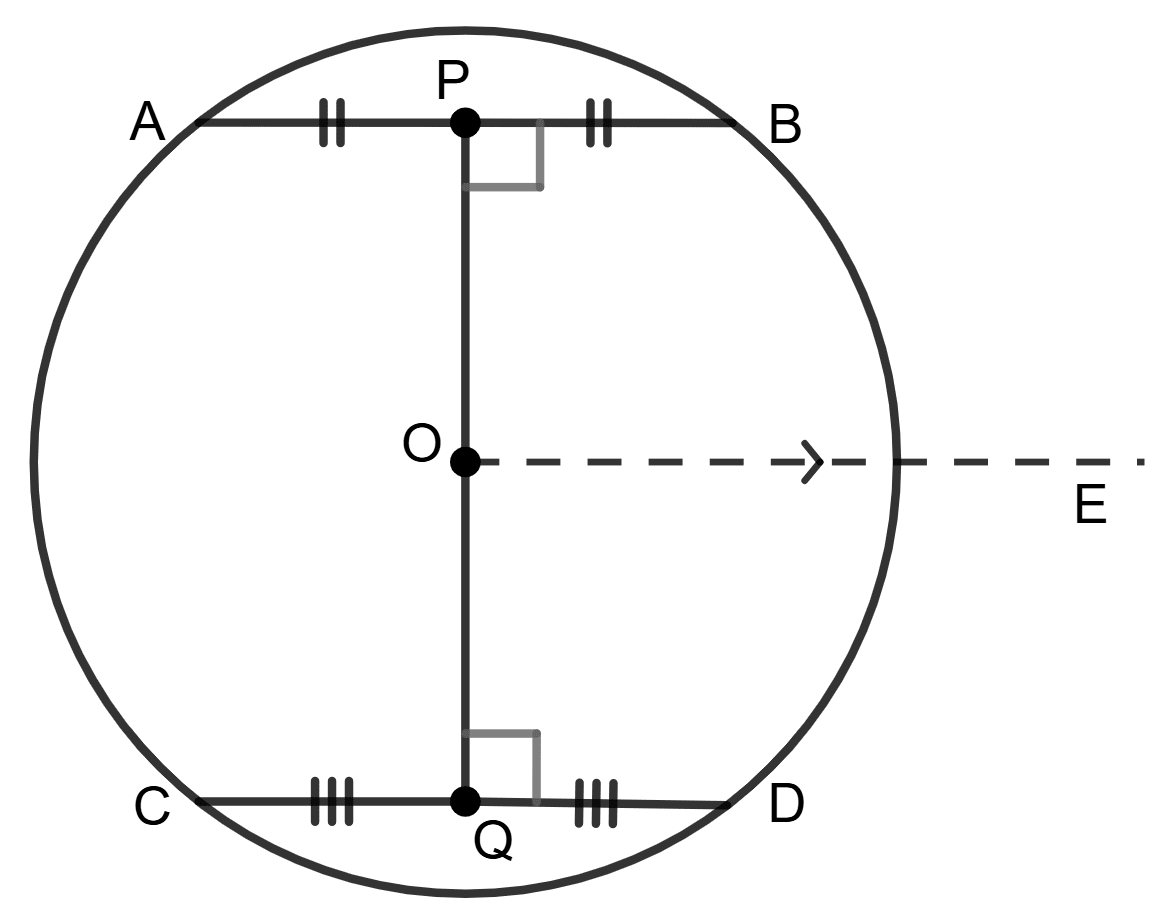
Let AB and CD be two parallel chords of a circle with center O. P is mid-point of AB and Q is mid-point of CD.
We have to prove that the line joining the points P and Q passes through the center O, i.e., ∠ POQ = 180°.
Construction : Join OP and OQ. Also, draw OE parallel to AB and CD.
Proof : Since, line segment joining the mid-point of the chord with the center of the circle is perpendicular to the chord, therefore, OP is perpendicular to AB and OQ is perpendicular to CD.
⇒ ∠ OPA = 90° and ∠ OQC = 90°
Now, OE ∥ AB and OP is transversal.
∴ ∠ POE = ∠ OPA = 90° (Alternate angles)
Similarly, OE ∥ CD and OQ is transversal.
∴ ∠ QOE = ∠ OQC = 90° (Alternate angles)
∴ ∠ POQ = ∠ POE + ∠ QOE
= 90° + 90°
= 180°
⇒ POQ is a straight line.
i.e, the line joining the mid-points of two parallel chords passes through the center.
∴ Assertion (A) is true.
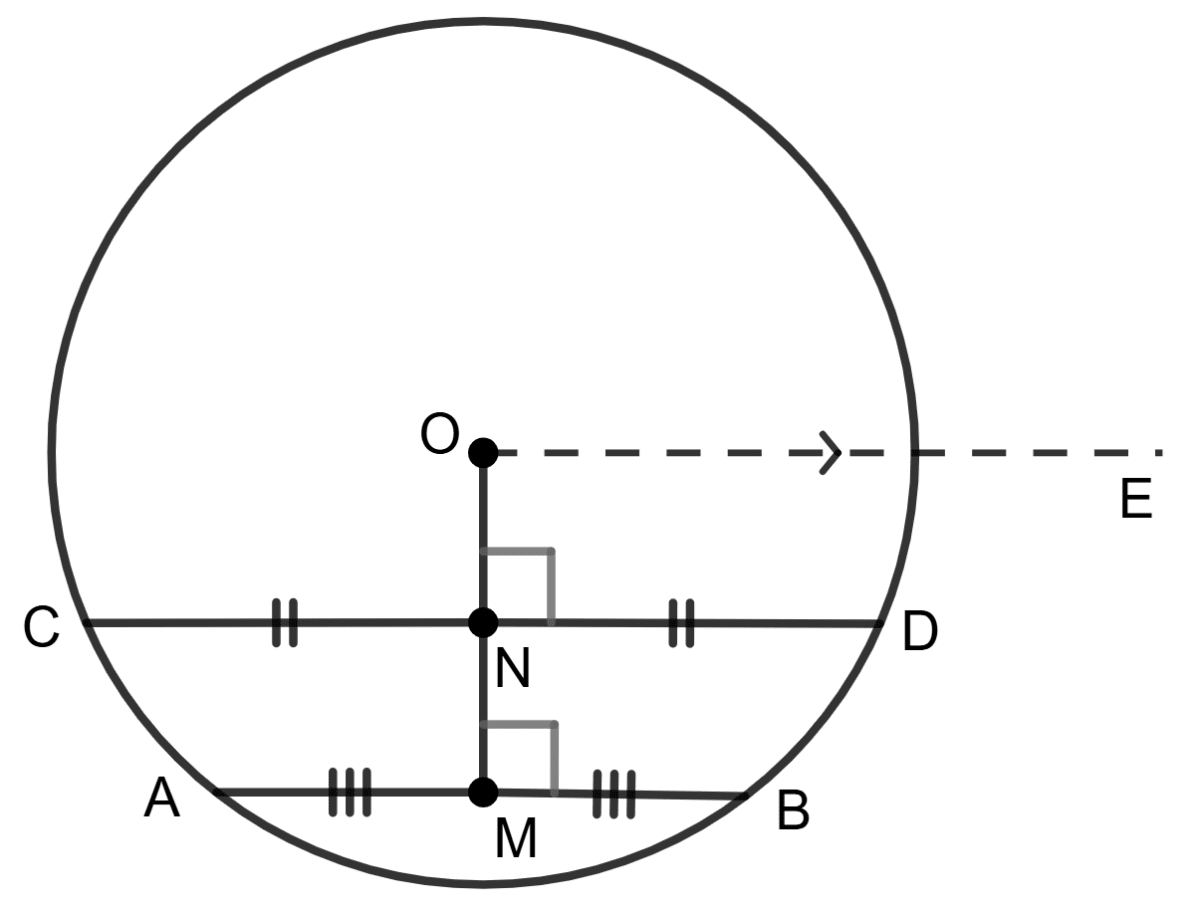
Let AB and CD be two parallel chords that are lying on the same side of a circle with center O. M is mid-point of AB and N is mid-point of CD.
We have to prove that the line joining the points M and N passes through the center O, i.e., ∠ MNO = 180°.
Construction : Join OM and ON. Also, draw OE parallel to AB and CD.
Proof : Since, line segment joining the mid-point of the chord with the center of the circle is perpendicular to the chord, therefore, OM is perpendicular to AB and ON is perpendicular to CD.
⇒ ∠ OMA = 90° and ∠ ONC = 90°
Now, OE ∥ AB and OM is transversal.
∴ ∠ MOE = ∠ OMA = 90° (Alternate angles)
Similarly, OE ∥ CD and ON is transversal.
∴ ∠ NOE = ∠ ONC = 90° (Alternate angles)
∴ ∠ MNO = ∠ MND + ∠ DNO
= ∠ MNC + ∠ CNO
= 90° + 90°
= 180°
⇒ MNO is a straight line.
i.e, The line passing through M and N also passes through O.
∴ Reason (R) is false.
Hence, Assertion (A) is true, Reason (R) is false.
Answered By
3 Likes
Related Questions
Assertion (A): AM and BN are tangents to the same circle at points A and B respectively. Then AN = BM.
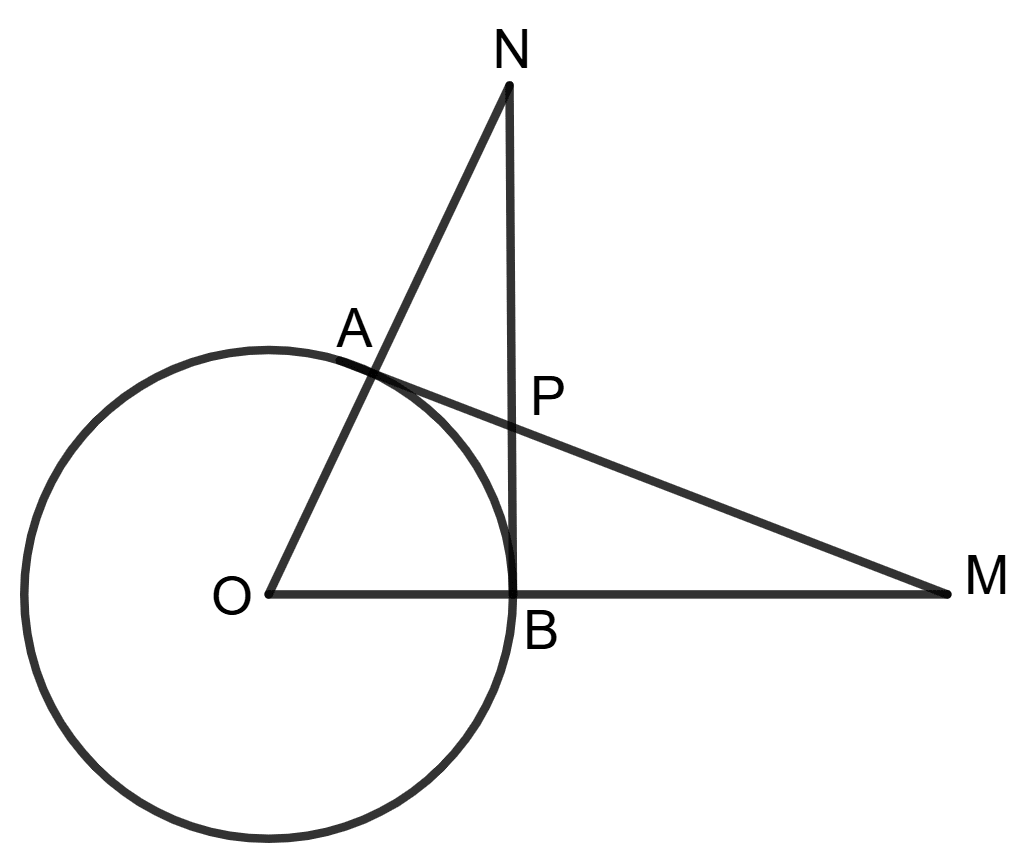
Reason (R): Since, tangents to a circle are equal in length
⇒ AM = BN
△APN ≅ △BPM ⇒ AN = BM
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A):
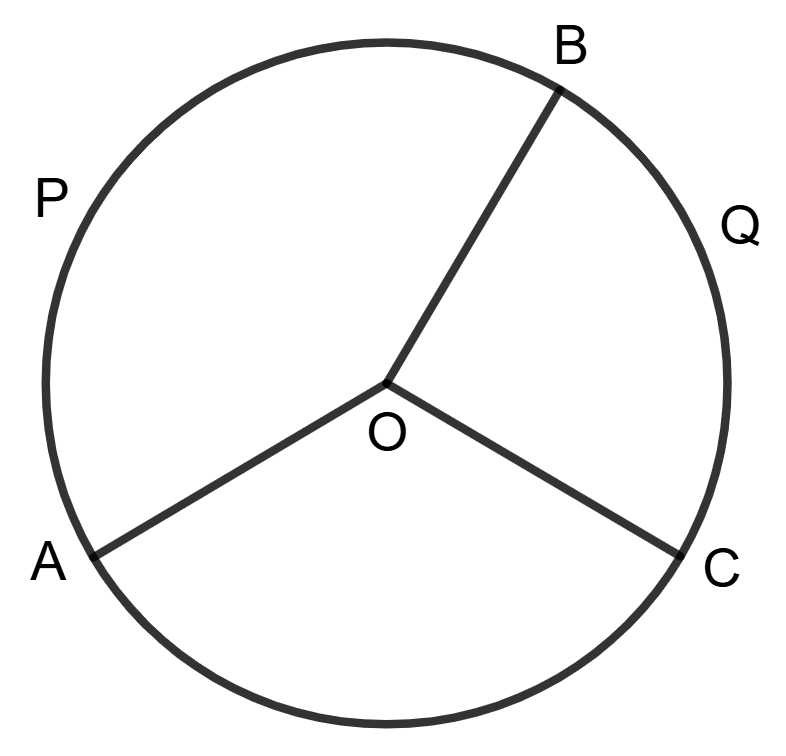
Arc APB : arc APBQC = 5 : 7
and reflex ∠AOC = 210°
then ∠AOB = 150°Reason (R):
=- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): In the given figure the lengths of arc AB and arc BC are in the ratio 2:1. If ∠AOB = 96°, then ∠AOC = 144°.
Reason (R): In two equal (congruent) circles if two arcs are equal, then they subtend equal angles at their centres.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): The median of : 25, 16, 26, 32, 31, 19, 28, 35 is 31.
Reason (R): To find median of the given data, the variate: x1, x2 , x3, ……………, xn needs to be arranged in ascending or descending order.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.