Mathematics
Assertion (A): In the given figure the lengths of arc AB and arc BC are in the ratio 2:1. If ∠AOB = 96°, then ∠AOC = 144°.
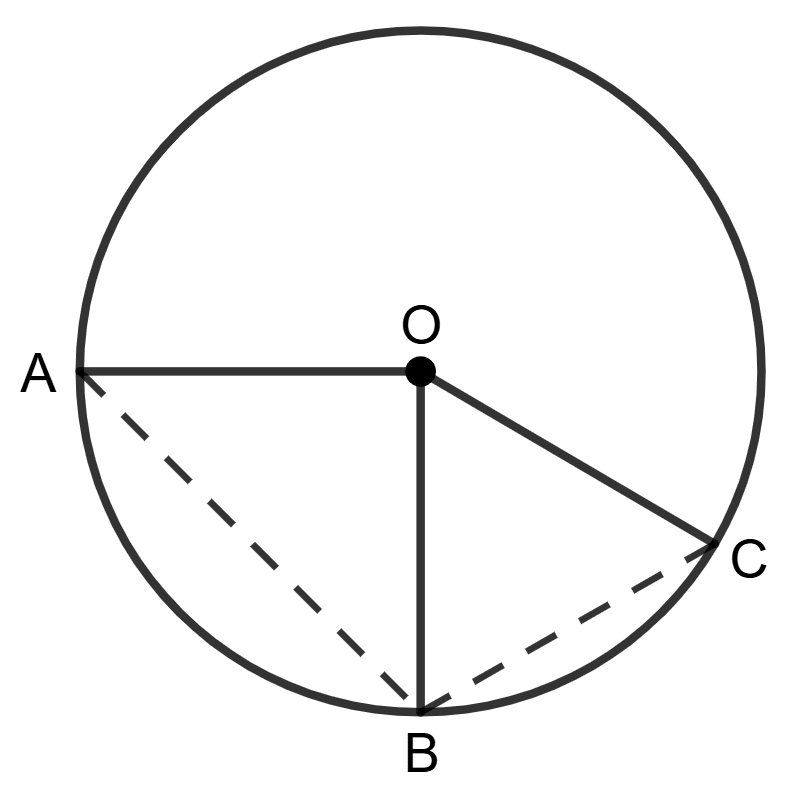
Reason (R): In two equal (congruent) circles if two arcs are equal, then they subtend equal angles at their centres.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Circles
1 Like
Answer
Both A and R are true.
Explanation
Given,
Arc AB : Arc BC = 2:1.
And, ∠AOB = 96°
To find : ∠AOC
Let x be the central angle of arc BC. Then, the central angle of arc AB is 2x.
So, 2x = 96°
⇒ x =
⇒ x = 48°
∠ BOC = 48°
⇒ ∠ AOC = ∠ AOB + ∠ BOC
= 96° + 48°
= 144°
∴ Assertion (A) is true.
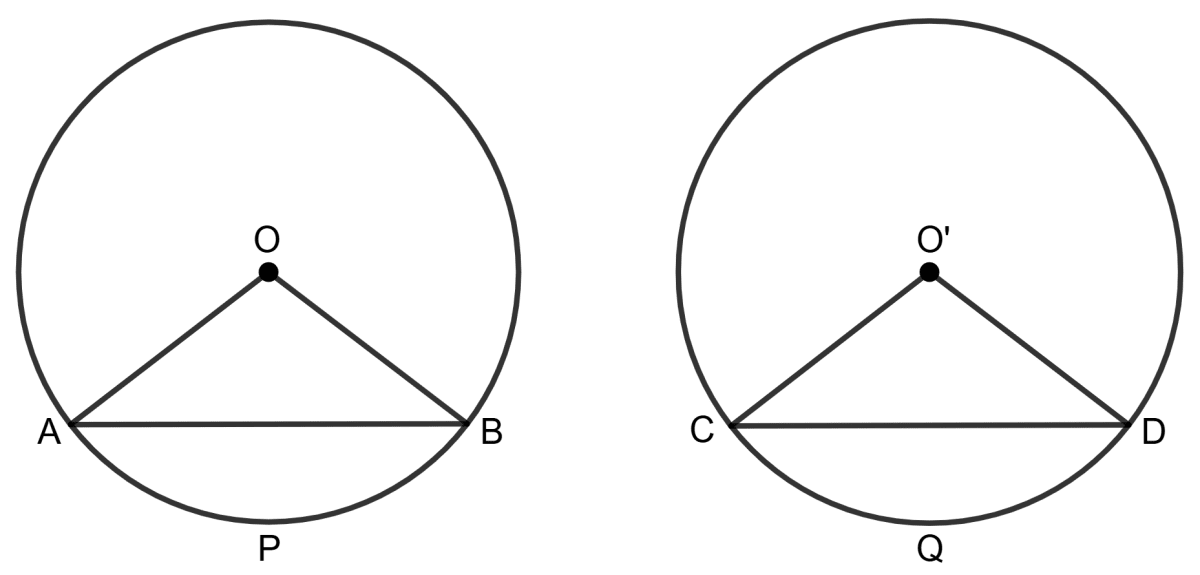
Given : Two circles with center O and O'. Arcs APB and CQD are equal in length.
To Prove : ∠ AOB = ∠ COD.
Construction : Draw chords AB and CD.
Proof : Since, two circles are congruent then equal arcs of a circle cut equal chords.
∴ arc APB = arc CQD
⇒ chord AB = chord CD
In Δ AOB and Δ COD,
OA = OC (Radii of the same circle)
OB = OD (Radii of the same circle)
AB = CD (Proved above)
By SSS Congruency Criterion,
Δ AOB ≅ Δ COD
By corresponding parts of congruent triangles,
∠ AOB = ∠ COD
∴ Reason (R) is true.
Hence, both Assertion (A) and Reason (R) are true.
Answered By
1 Like
Related Questions
Assertion (A):
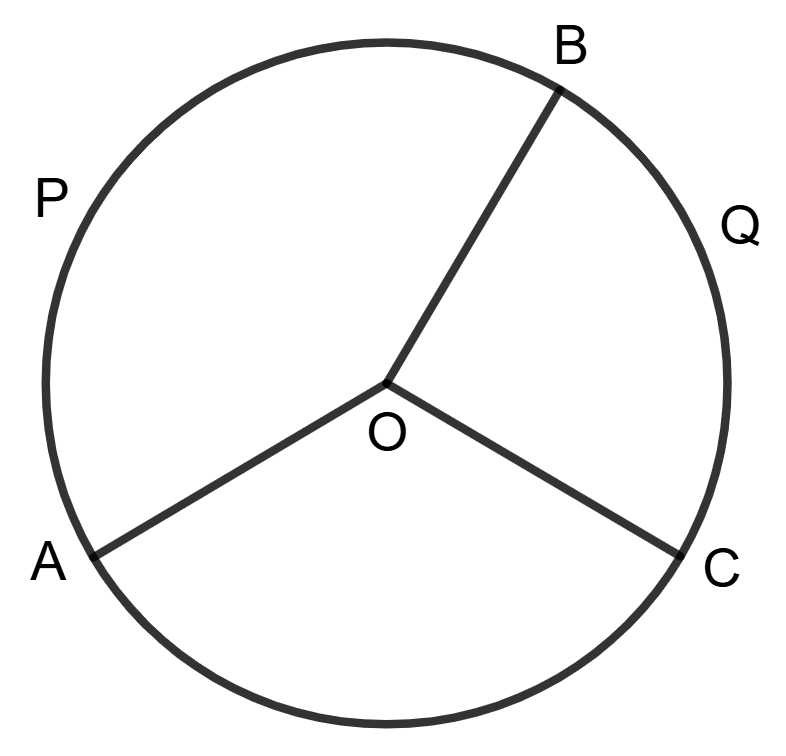
Arc APB : arc APBQC = 5 : 7
and reflex ∠AOC = 210°
then ∠AOB = 150°Reason (R):
=- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): The line segment joining the mid-points of all parallel chords of a circle passes through the centre.
Reason (R): If the chords are on same side of centre then only the line through the mid-points of the chords passes through the centre.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): The median of : 25, 16, 26, 32, 31, 19, 28, 35 is 31.
Reason (R): To find median of the given data, the variate: x1, x2 , x3, ……………, xn needs to be arranged in ascending or descending order.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): If the class marks of two overlapping intervals of equal size in a distribution are 94 and 104 then the corresponding intervals are 89-99, 99-109.
Reason (R): The class mark of a class interval
=
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.