Mathematics
Assertion (A): If the class marks of two overlapping intervals of equal size in a distribution are 94 and 104 then the corresponding intervals are 89-99, 99-109.
Reason (R): The class mark of a class interval
=
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Statistics
1 Like
Answer
Both A and R are true.
Explanation
Class mark =
Class mark for the first interval:
Let the lower limit be L1 and the upper limit be U1.
Using the formula,
94 =
⇒ L1 + U1 = 94 x 2
⇒ L1 + U1 = 188 ……………..(1)
Class mark for the second interval:
Let the lower limit of the second interval be L2 and the upper limit be U2.
Using the formula,
104 =
⇒ L2 + U2 = 104 x 2
⇒ L2 + U2 = 208 ……………..(2)
Since the intervals are of equal size and overlap, we can assume that the difference between the upper limit of the first interval and the lower limit of the second interval is the size of the interval.
U2 - L2 = U1 - L1 = Interval Size
From eq (1) and (2), the difference between the two class marks is:
104 - 94 = 10
Thus, the interval size is 10.
For the first interval:
L1 + U1 = 188,
U1 - L1 = 10
Adding these two equations:
(L1 + U1) + (U1 - L1) = 188 + 10
⇒ L1 + U1 + U1 - L1 = 198
⇒ 2U1 = 198
⇒ U1 =
⇒ U1 = 99
Thus, L1 = 188 - 99 = 89
For the second interval:
L2 + U2 = 208
U2 - L2 = 10
Adding these two equations:
(L2 + U2) + (U2 - L2) = 208 + 10
⇒ L2 + U2 + U2 - L2 = 218
⇒ 2U2 = 218
⇒ U2 =
⇒ U2 = 109
Thus, L2 = 208 - 109 = 99
The corresponding intervals are 89−99 and 99−109.
∴ Assertion (A) is true.
The class mark of a class interval is the midpoint of the interval, given by:
Class Mark =
∴ Reason (R) is true.
Hence, both Assertion (A) and Reason (R) are true.
Answered By
2 Likes
Related Questions
Assertion (A): In the given figure the lengths of arc AB and arc BC are in the ratio 2:1. If ∠AOB = 96°, then ∠AOC = 144°.
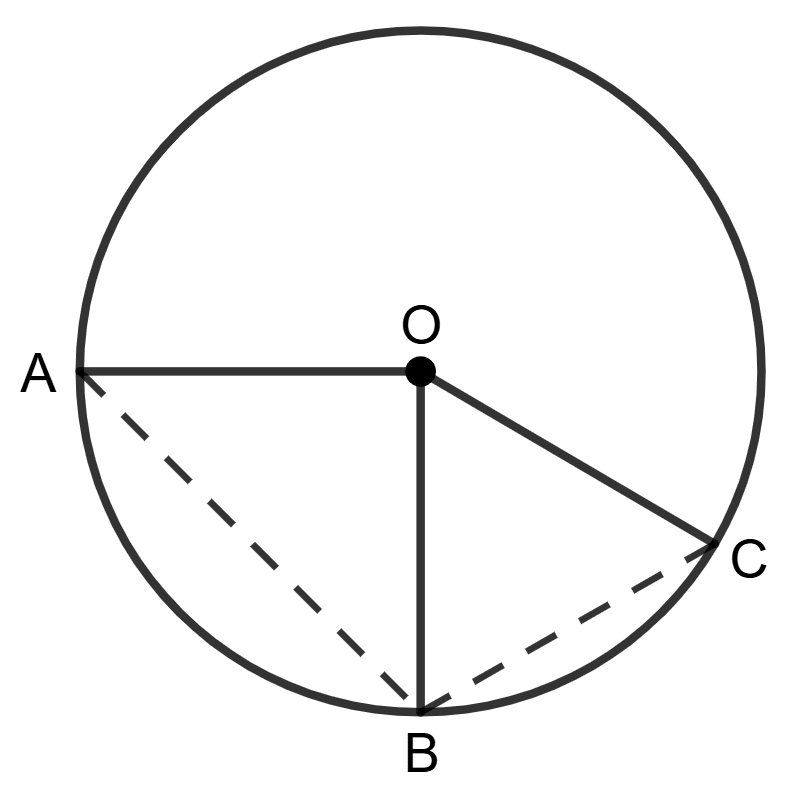
Reason (R): In two equal (congruent) circles if two arcs are equal, then they subtend equal angles at their centres.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): The median of : 25, 16, 26, 32, 31, 19, 28, 35 is 31.
Reason (R): To find median of the given data, the variate: x1, x2 , x3, ……………, xn needs to be arranged in ascending or descending order.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): In a frequency distribution the class marks are 5, 15 and 25. The corresponding class-intervals are 5 - 15 and 15 - 25.
Reason (R): ∵ and
∴ Class-intervals are : (5 - 5) - (5 + 5), (15 - 5) - (15 + 5) and (25 - 5) - (25 + 5)- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A):
Class interval Frequency Cumulative Frequency 0 - 5 5 5 5 - 10 9 14 10 - 15 a 22 15 - 20 6 28 20 - 25 10 b ⇒ a = 22 and b = 10
Reason (R):
14 + a = 22 ⇒ a = 8
28 + 10 = b ⇒ b = 38- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.