Assertion (A): If log₁₀x $\times$ log₁₀5 = log₁₀20
⇒ 5x = 20 and x = 4

Reason (R): If log₁₀x $\times$ log₁₀5 = log₁₀20
⇒ x + 5 = 20 and x = 15

1. A is true, R is false.
2. A is false, R is true.
3. Both A and R are true.
4. Both A and R are false.

Assertion (A):

$\dfrac{1}{2}$ log₂₅ $5+\dfrac{1}{3}$ log₈2 = $\dfrac{13}{36}$.

Reason (R):

$\dfrac{1}{2}$ log₂₅ $5+\dfrac{1}{3}$ log₈2 = $\dfrac{1}{4}+\dfrac{1}{9}=\dfrac{13}{36}$

1. A is true, R is false.
2. A is false, R is true.
3. Both A and R are true.
4. Both A and R are false.

Assertion (A): log₁₀₀(1000) = $\dfrac{3}{2}$.

Reason (R): log_b a = $\dfrac{log_{x}a}{log{x}b}$, for all a, b, x.

1. A is true, R is false.
2. A is false, R is true.
3. Both A and R are true.
4. Both A and R are false.

Assertion (A): Using the information in the given figure; we get BD = CE.

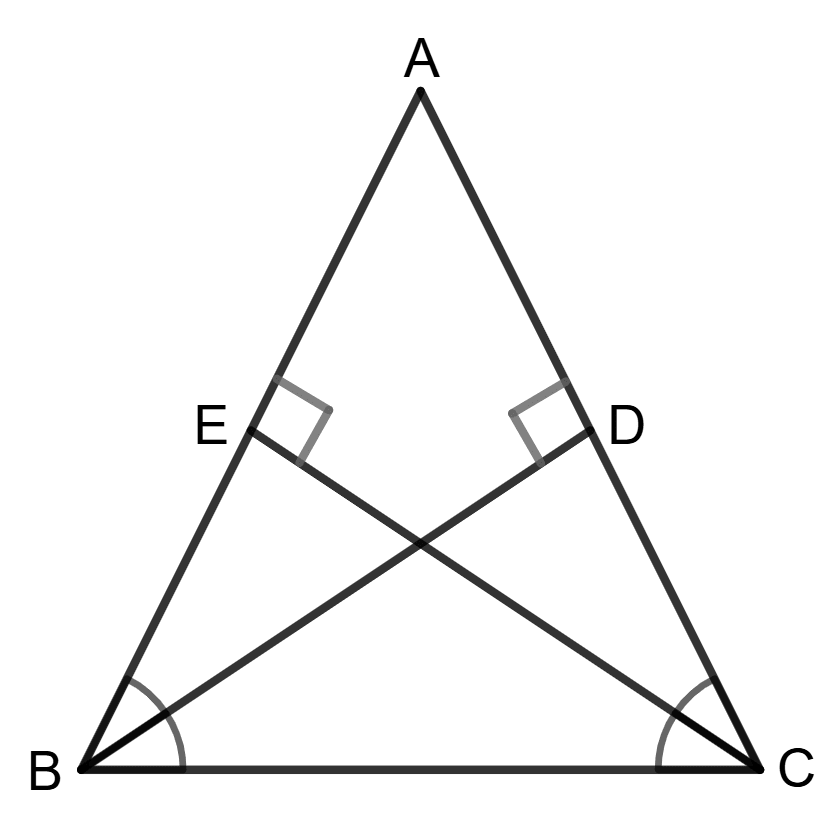
Reason (R):

∵ △BDC ≅ △CEB (By AAS or ASA)
BD = CE

1. A is true, R is false.
2. A is false, R is true.
3. Both A and R are true.
4. Both A and R are false.