Mathematics
Assertion (A): Using the information in the given figure; we get BD = CE.
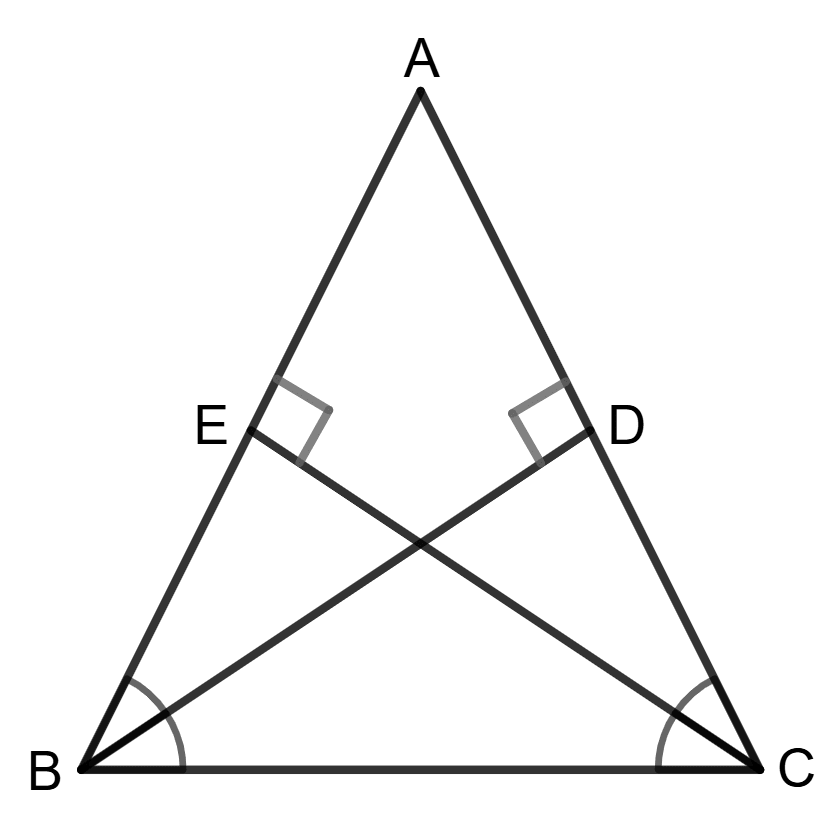
Reason (R):
∵ △BDC ≅ △CEB (By AAS or ASA)
BD = CE
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Triangles
1 Like
Answer
Both A and R are true.
Explanation
In Δ BDC and Δ CEB,
∠ BDC = ∠ CEB (both are right angle)
∠ DBC = ∠ ECB (∠ ABC = ∠ ACB ⇒ ∠ ABC = ∠ ACB ⇒ ∠ DBC = ∠ ECB)
BC = BC (Common angles)
So, using the ASA Congruency criterion,
Δ BDC ≅ Δ CEB
Hence, their corresponding sides are equal i.e, BD = CE.
∴ Assertion (A) is true.
As proved in the assertion, BD = CE.
∴ Reason (R) is true.
Hence, both Assertion (A) and Reason (R) are true.
Answered By
1 Like
Related Questions
Assertion (A): logx (m x n x p) = logx m + logx n + log p.
Reason (R): The logarithm of a product at any non-zero base is equal to the sum of the logarithms of its factors at the same base.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): log100(1000) = .
Reason (R): logb a = , for all a, b, x.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Using the information in the given figure, we get AM = CN.
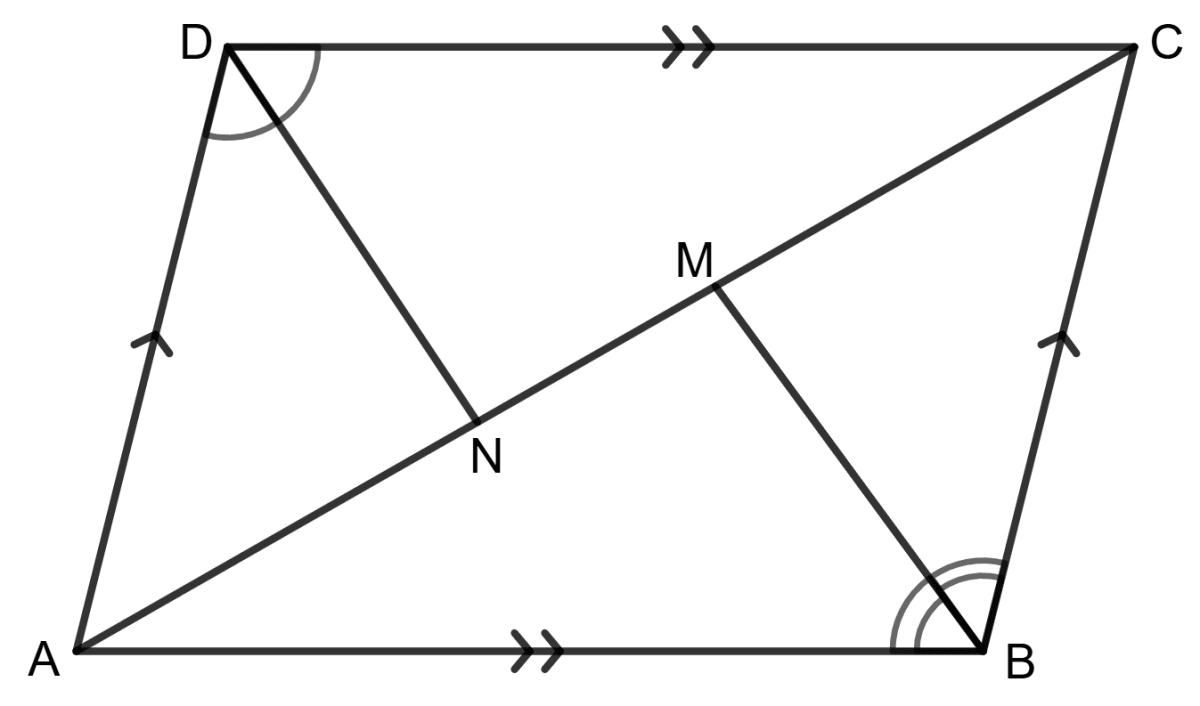
Reason (R):
∠NDC = ∠ADC
and, ∠MBC = ∠ABC
Since. ∠ADC = ∠ABC
⇒ ∠NDC = ∠MBC
⇒ ∠AM = CN- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): The straight line drawn through the mid-point of one side of a triangle and parallel to another side bisects the third side.
Reason (R): If a transversal makes equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.