Case Study

The union of the set of rational numbers (Q) and irrational numbers (P) form the set of real numbers (R). Rational numbers are the set of numbers which can be written in the form of $\dfrac{a}{b}$, where a and b are integers and b is not equal to zero. The decimal expansion of a rational number is either terminating or non-terminating repeating. The number which cannot be expressed in the form $\dfrac{a}{b}$ are called irrational numbers. The decimal expansion of irrational numbers is non-terminating non-repeating.

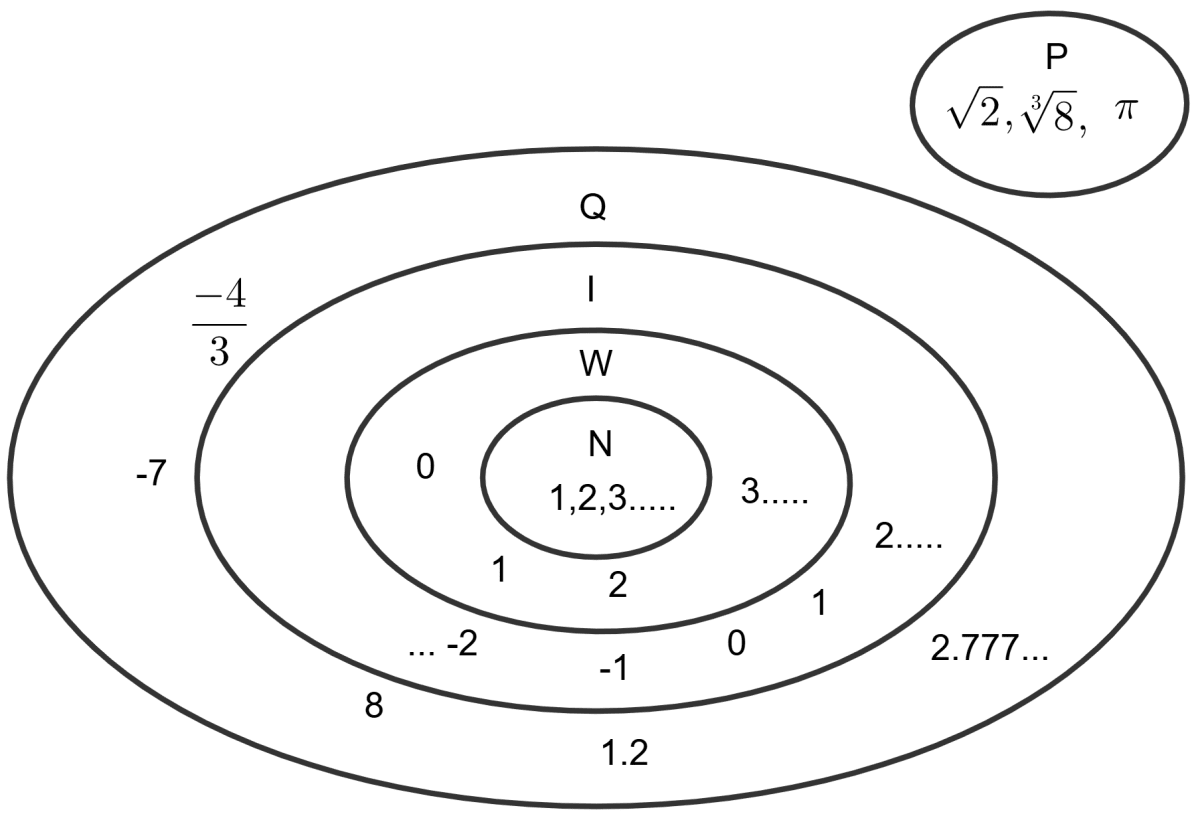
Based on this information, answer the following questions:

1. Every rational number is:
   (a) a natural number
   (b) a whole number
   (c) an integer
   (d) a real number

2. Every real number is:
   (a) an integer
   (b) a rational number
   (c) an irrational number
   (d) either a rational number or an irrational number.

3. The sum of two irrationals is:
   (a) irrational
   (b) rational
   (c) either rational or irrational
   (d) neither rational or irrational.

4. The product of a rational and irrational number is:
   (a) an irrational number
   (b) a rational number
   (c) either a rational number or an irrational number
   (d) neither a rational number nor an irrational number.

5. The number of irrational number is:
   (a) finite
   (b) infinite
   (c) neither finite or infinite
   (d) none of these.

Case Study

Ms Mehta teaches maths in a school. One day after teaching the lesson of number system, she wanted to check the understanding of the students of her class. So, she wrote two numbers, $\dfrac{3}{11}\text{ and } 0.\overline{52}$ on the blackboard and asked few questions based on them. You please try to answer the following questions asked by Ms Mehta.

1. The decimal expansion of $\dfrac{3}{11}$ is:
   (a) terminating
   (b) non-terminating
   (c) non-terminating non-repeating
   (d) non-terminating repeating

2. $0.\overline{52}$ is:
   (a) non-terminating non-repeating
   (b) non-terminating repeating
   (c) non-terminating
   (d) terminating

3. The decimal form of $\dfrac{3}{11}$:
   (a) 0.27
   (b) 0.2727
   (c) $0.\overline{27}$
   (d) 0.3

4. $0.\overline{52}$ as vulgar fraction becomes:
   
   (a) $\dfrac{52}{99}$
   
   (b) $\dfrac{52}{100}$
   
   (c) $\dfrac{26}{25}$
   
   (d) $\dfrac{13}{25}$

5. The sum of $0.\overline{52} \text{ and } \dfrac{3}{11}$ is :
   (a) $\dfrac{79}{99}$
   
   (b) $\dfrac{70}{99}$
   
   (c) $\dfrac{52}{99}$
   
   (d) $\dfrac{40}{99}$

Assertion (A): Each of the numbers $\sqrt[3]{2}, \sqrt[3]{3}, \sqrt[3]{4}, \sqrt[3]{5}, \sqrt[3]{6}, \sqrt[3]{7}$ is irrational.

Reason (R): The cube roots of all natural numbers is irrational.

1. A is true, R is false

2. Both A and R are true

3. A is false, R is true

4. Both A and R are false.

The sum of all rational numbers between 0 and 0.1 is :

1. finite

2. infinite

3. can't say anything

4. none of these