Mathematics
Assertion (A) : The numbers 8, 10, 12, x and 15 are in ascending order of their values. If the mean of their observations is equal to their median, the value of x is 15.
Reason (R) : If the number of observations is n, their mean = and median (if n is odd) = value of the observation
A is true, R is true
A is true, R is false
A is false, R is true
A is false, R is false
Statistics
5 Likes
Answer
Numbers : 8, 10, 12, x and 15.
n = 5, which is odd
Median = = 3rd term = 12.
Given,
Mean = Median
= 12
⇒ 45 + x = 60
⇒ x = 60 - 45 = 15.
By formula,
If the number of observations is n, their mean = and median (if n is odd) = value of the observation.
∴ A and R both are true.
Hence, Option 1 is the correct option.
Answered By
2 Likes
Related Questions
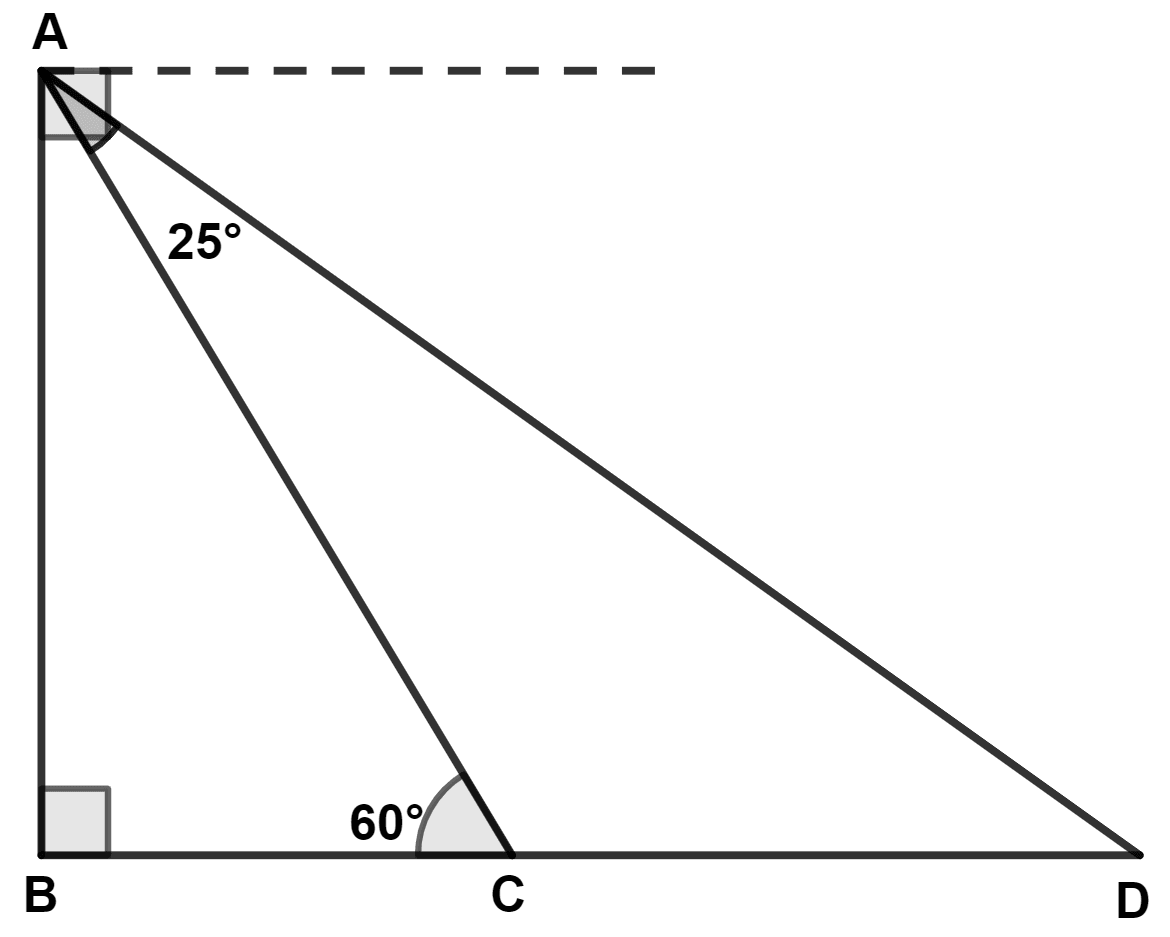
In the given figure, the angle of depression of point D from point A is :
55°
35°
45°
60°
Two men A and B have a choice to buy ₹ 100 shares. A buys shares at ₹ 120 per share and 5% dividend. B buys shares at ₹ 150 per share and 8% dividend. Which of the two men A and B gets the better return, if the nominal value of both the shares is ₹ 100?
A
B
both get equal returns
cannot say
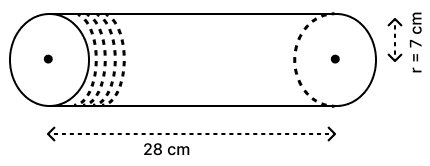
As shown in the adjoining figure, a wire of uniform thickness is rolled on a cylinder to cover it completely, without any overlapping. If the diameter of the wire is 0.25 cm, find :
(i) the number of turns made by the wire to cover the cylinder completely.
(ii) length of wire used.
Asit saves ₹ 50 daily and deposits ₹ 1,500 every month in a recurring deposit account for years at r% per annum. If he gets ₹ 50,812.50 on maturity, find the value of r.