In a pie-chart, the angle corresponding to different components is :

1. $\dfrac{\text{value of the component}}{\text{total value of all the components}} \times 360°$

2. $\dfrac{\text{total value of all the components}}{\text{value of the component}} \times 360°$

3. total value of all the components x value of the component x 360°

4. $\dfrac{360°}{\text{total value of all the components} \times \text{value of the component}}$

Consider the following class intervals of a grouped data :

Statement 1: Class marks of the 3^rd class intervals is 46.5.

Statement 2: If the class mark of 2^nd interval is 77.5, the interval is 60 - 85.

Which of the following options is correct?

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Assertion (A) : Class size of the following class intervals is 10.

1 - 10, 11 - 20, 21 - 30, etc.

Reason (R) : The difference between the upper limit and lower limit is the class size.

1. Both A and R are correct, and R is the correct explanation for A.

2. Both A and R are correct, and R is not the correct explanation for A.

3. A is true, but R is false.

4. A is false, but R is true.

Assertion (A) : The given bar graph shows the heights of six mountain peaks.

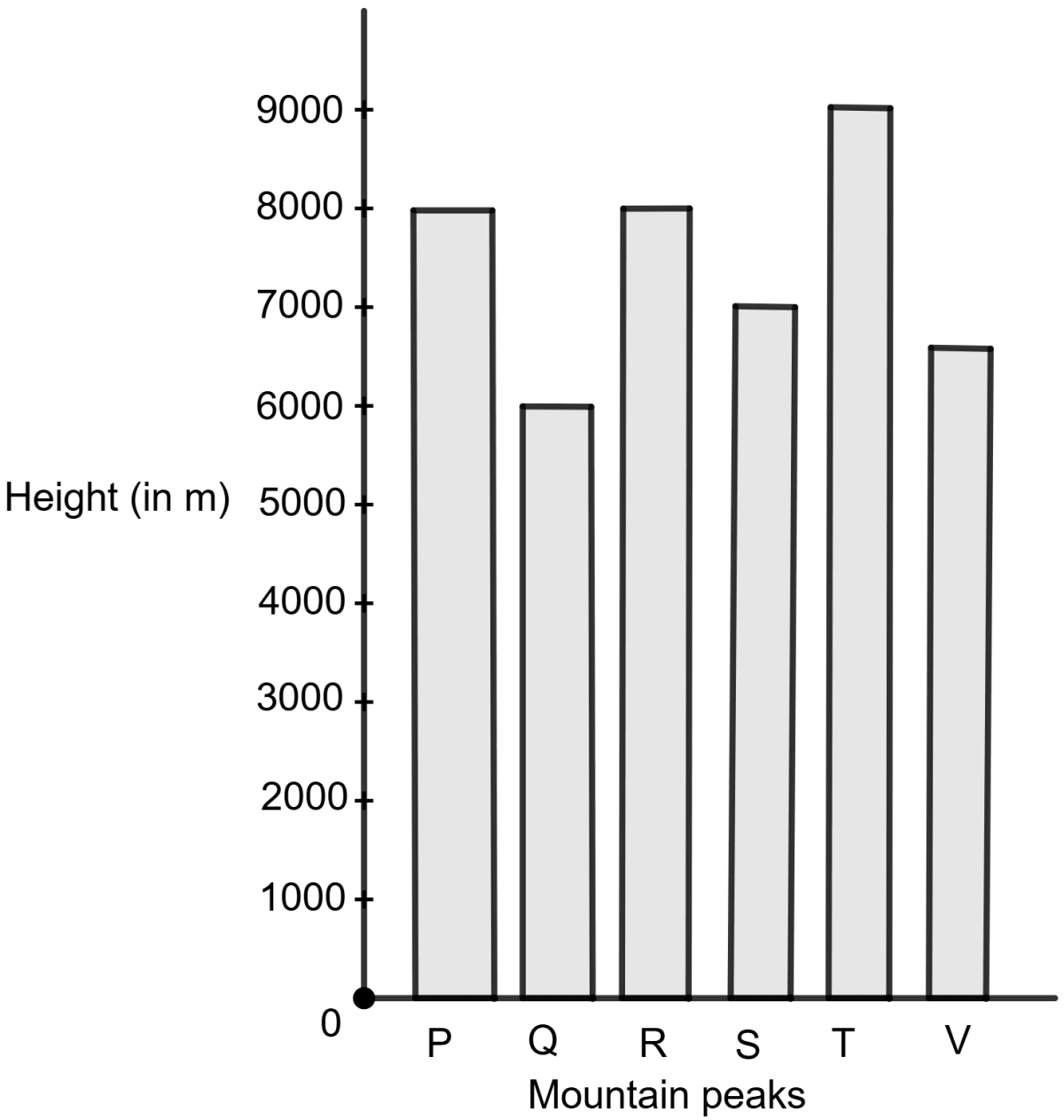
The ratio of height of the highest to the lowest peak is 3 : 2.

Reason (R) : The space between consecutive bars may be of any suitable value, but the spaces between all the consecutive bars must the same.

1. Both A and R are correct, and R is the correct explanation for A.

2. Both A and R are correct, and R is not the correct explanation for A.

3. A is true, but R is false.

4. A is false, but R is true.