Mathematics
Assertion (A): A triangle with sides 2 cm, 3 cm, 4 cm is not a right angled triangle.
Reason (R): A triangle with sides 2 cm, 3 cm, 4 cm is a scalene triangle.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
Given the sides: a = 2 cm, b = 3 cm, c = 4 cm.
The longest side is c = 4 cm.
Let's check if c2 = a2 + b2
Taking L.H.S.,
c2 = 42 = 16.
Taking R.H.S.,
a2 + b2 = 22 + 32
= 4 + 9
= 13.
Since 16 ≠ 13, the condition for a right-angled triangle is not met.
Therefore, the triangle with sides 2 cm, 3 cm, 4 cm is not a right-angled triangle.
∴ Assertion (A) is true.
A scalene triangle is defined as a triangle in which all three sides have different lengths.
Given the side lengths are 2 cm, 3 cm, and 4 cm. All three lengths are distinct.
∴ Reason (R) is true.
∴ Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Hence, option 4 is the correct option.
Related Questions
Assertion (A): If the sides of a rectangular plot are 80 m and 60 m, then the length of its diagonal is 100 m.
Reason (R): In a rectangle, all angles are 90°.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Assertion (A): If triangle ABC is isosceles with AC = BC and AB2 = 2AC2, then triangle ABC is right angled.
Reason (R): If in a triangle ABC, we have AB2 = 2AC2 then we can conclude that it is right angled triangle.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
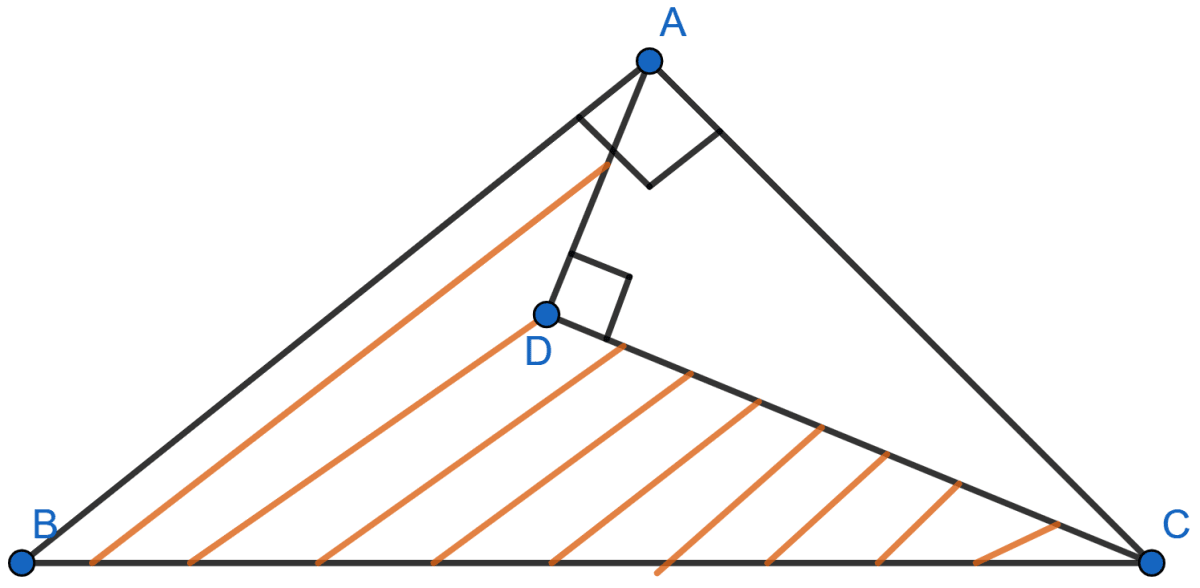
In the figure given below, AD ⊥ BC, AB = 25 cm, AC = 17 cm and AD = 15 cm. Find the length of BC.

In the figure given below, ∠BAC = 90°, ADC = 90°, AD = 6 cm, CD = 8 cm and BC = 26 cm. Find
(i) AC
(ii) AB
(iii) area of the shaded region.