Mathematics
Assertion (A): Two circles touch each other externally. The sum of their areas is 74π cm2 and distance between their centres is 12 cm. Then difference between their radii is 2 cm.
Reason (R): When two circles touch each other internally, then two centres and point of contact lie on the same line and distance between their centres equals to the difference between two radii.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Mensuration
3 Likes
Answer
Both A and R are true.
Explanation
Let r1 and r2 be the radii of two circles.
Sum of their areas = 74π cm2
⇒ πr12 + πr22 = 74π
⇒ π(r12 + r22) = 74π
⇒ r12 + r22 = 74 ……………..(1)
Distance between their centres = 12 cm.
⇒ r1 + r2 = 12
⇒ r1 = 12 - r2
Substituting r1 = 12 - r2 into equation (1),
⇒ (12 - r2)2 + r22 = 74
⇒ (12)2 + r22 - 2 x 12 x r2 + r22 = 74
⇒ 144 + 2r22 - 24r2 = 74
⇒ 144 + 2r22 - 24r2 - 74 = 0
⇒ 2r22 - 24r2 + 70 = 0
⇒ r22 - 12r2 + 35 = 0
⇒ r22 - (7r2 + 5r2) + 35 = 0
⇒ r22 - 7r2 - 5r2 + 35 = 0
⇒ (r22 - 7r2) - (5r2 - 35) = 0
⇒ r2(r2 - 7) - 5(r2 - 7) = 0
⇒ (r2 - 7)(r2 - 5) = 0
⇒ r2 = 7 or 5
If r2 = 7, then r1 = 12 - 7 = 5
If r2 = 5, then r1 = 12 - 5 = 7
The difference between the radii is 2 cm.
∴ Assertion (A) is true.
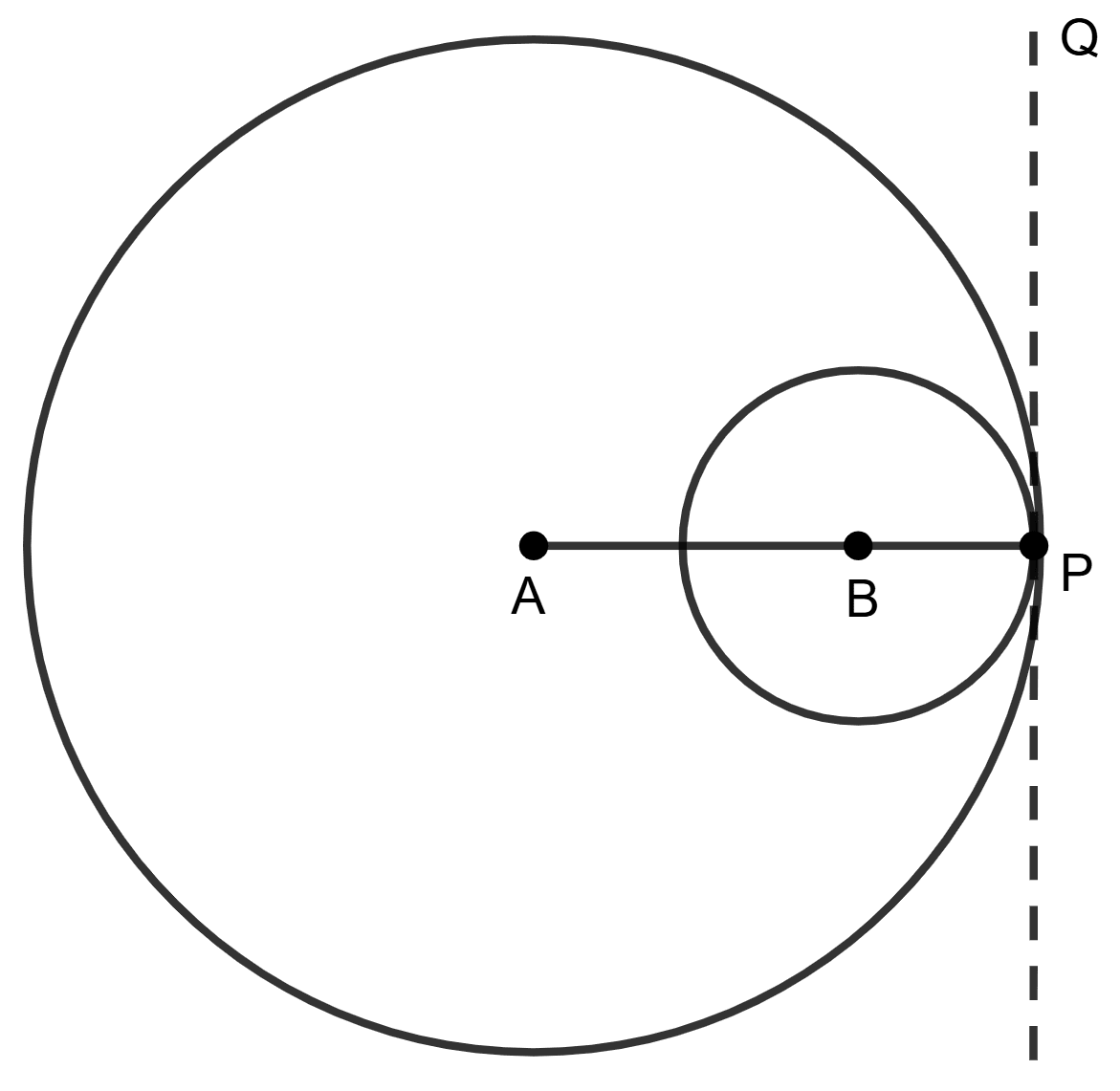
Given: Two circles with centers A and B touching each other internally at point P.
To Prove : P lies on the line AB produced.
Construction : Through the point of contact P, draw a common tangent PQ. Join AP and BP.
Proof : Angles between the radius and tangent are always 90°.
So, ∠ APQ = 90° and ∠ BPQ = 90°
∴ AP and BP both are perpendicular to the tangent PQ at the same point P.
Only one perpendicular can be drawn to a line through a point in it.
AP and BP lie in the same line.
⇒ ABP is a straight line.
∴ P lies on the line AB (when produced)
∴ Reason (R) is true.
Hence, both Assertion (A) and Reason (R) are true.
Answered By
1 Like
Related Questions
Assertion (A): The ratio between radius and area of a circle is 7 : 44. If the radius of this circle is doubled, the ratio between the new radius and area of the resulting circle will be 7 : 176.
Reason (R): Given :
∴
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): One pair of opposite sides of a parallelogram are 15 cm each. If the distance between other pair of opposite sides is 8 cm, then area of the parallelogram = 120 cm2.
Reason (R): Area of parallelogram = Base x Corresponding height
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): The ratio between the edges of three cubes is 2 : 3 : 4. The ratio between their volumes is 4 : 9 : 16.
Reason (R): The ratio between their volumes = 23 : 33 : 43 = 8 : 27 : 64.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): The internal area of cross-section of a pipe is 21 cm2. Water runs through this pipe at a speed of 5 km/h. The volume of water that runs through the pipe in 2 minutes = 21 cm2 x 5 km/h x 2 minutes
Reason (R): The volume of water that runs through the pipe in 2 minutes = area of cross-section in cm2 x speed of water through it in cm/s x time in seconds
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.