Mathematics
Assertion (A): The ratio between radius and area of a circle is 7 : 44. If the radius of this circle is doubled, the ratio between the new radius and area of the resulting circle will be 7 : 176.
Reason (R): Given :
∴
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Mensuration
2 Likes
Answer
A is true, R is false.
Explanation
Let r be the radius of the circle.
If the radius of this circle is doubled,
r' = 2r = 2 x 2 = 4
∴ Assertion (A) is true.
Given :
∴ Reason (R) is false.
Hence, Assertion (A) is true, Reason (R) is false.
Answered By
1 Like
Related Questions
Assertion (A): The mean of 5 observations is 30. On excluding one of these observations, the mean of the remaining observation is increased to 31. The excluded observation is
= 5 x 30 - 4 x 31 = 150 - 124 = 26
Reason (R): The excluded observation is = 5 x 31 - 4 x 30 = 155 - 120 = 35
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): When each side of a square is increased by 5 cm, its area increases by 75 sq. cm. The side of the square is 5 cm.
Reason (R):
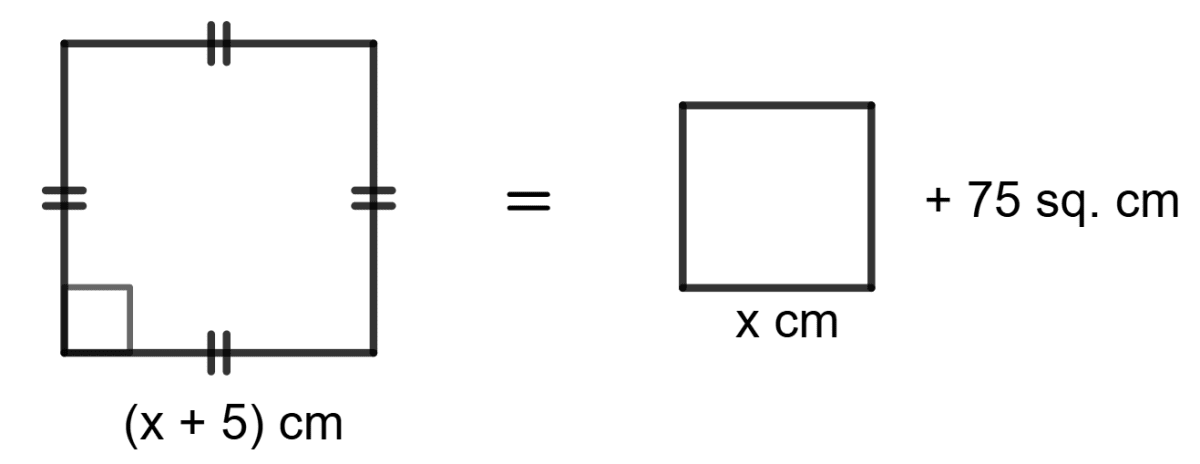
⇒ (x+5)2 = x2 + 75 ⇒ x = 5cm
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): One pair of opposite sides of a parallelogram are 15 cm each. If the distance between other pair of opposite sides is 8 cm, then area of the parallelogram = 120 cm2.
Reason (R): Area of parallelogram = Base x Corresponding height
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Two circles touch each other externally. The sum of their areas is 74π cm2 and distance between their centres is 12 cm. Then difference between their radii is 2 cm.
Reason (R): When two circles touch each other internally, then two centres and point of contact lie on the same line and distance between their centres equals to the difference between two radii.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.