Mathematics
Assertion (A): The mean of 5 observations is 30. On excluding one of these observations, the mean of the remaining observation is increased to 31. The excluded observation is
= 5 x 30 - 4 x 31 = 150 - 124 = 26
Reason (R): The excluded observation is = 5 x 31 - 4 x 30 = 155 - 120 = 35
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Statistics
1 Like
Answer
A is true, R is false.
Explanation
Given,
Mean = 30
Number of all observations = 5
Mean =
⇒ 30 =
⇒ Sum of all 5 observations = 30 x 5 = 150
After excluding one observation, the new mean of the remaining 4 observations is 31:
Number of all observations = 4
⇒ 31 =
⇒ Sum of all 4 observations = 31 x 4 = 124
Sum of all 5 observations = Sum of all 4 observations + Excluded observation
⇒ 150 = 124 + Excluded observation
⇒ Excluded observation = 150 - 124
⇒ Excluded observation = 26
∴ Assertion (A) is true.
From the above calculation,
The excluded observation is 26.
According to Reason, the excluded observation is = 5 x 31 - 4 x 30 = 155 - 120 = 35 (≠ 26)
∴ Reason (R) is false.
Hence, Assertion (A) is true, Reason (R) is false.
Answered By
1 Like
Related Questions
Assertion (A):
Class interval Frequency Cumulative Frequency 0 - 5 5 5 5 - 10 9 14 10 - 15 a 22 15 - 20 6 28 20 - 25 10 b ⇒ a = 22 and b = 10
Reason (R):
14 + a = 22 ⇒ a = 8
28 + 10 = b ⇒ b = 38- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): The median of a certain set of data is 42. If each data in the set is first increased by 7 and then the result is multiplied by 3, the new median is = (42 + 7) x 3 = 147
Reason (R): The resulting median = 42 + 7 x 3 = 42 + 21 = 63
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): When each side of a square is increased by 5 cm, its area increases by 75 sq. cm. The side of the square is 5 cm.
Reason (R):
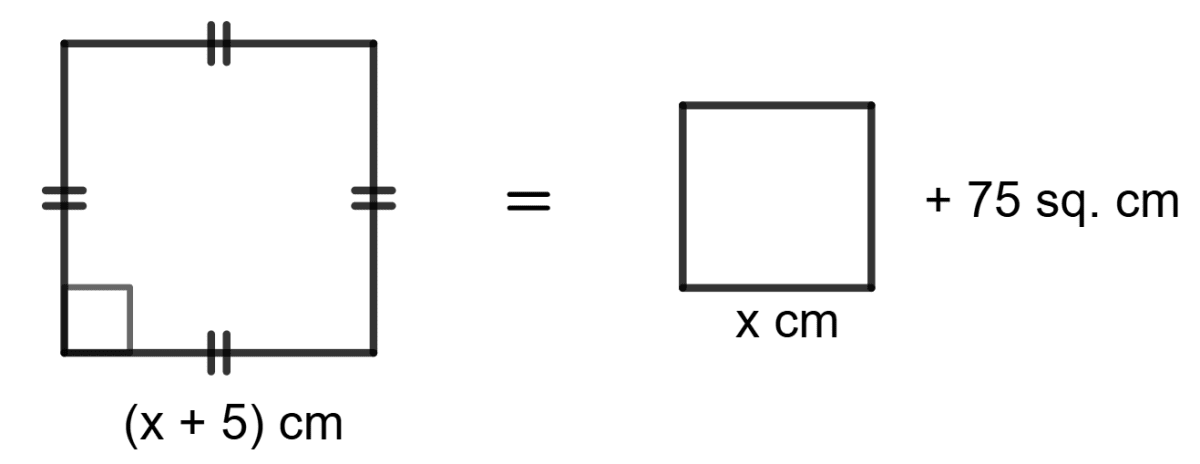
⇒ (x+5)2 = x2 + 75 ⇒ x = 5cm
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): The ratio between radius and area of a circle is 7 : 44. If the radius of this circle is doubled, the ratio between the new radius and area of the resulting circle will be 7 : 176.
Reason (R): Given :
∴
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.