Mathematics
Assertion (A): Using the information in the given figure, we get BC > AB > AC.
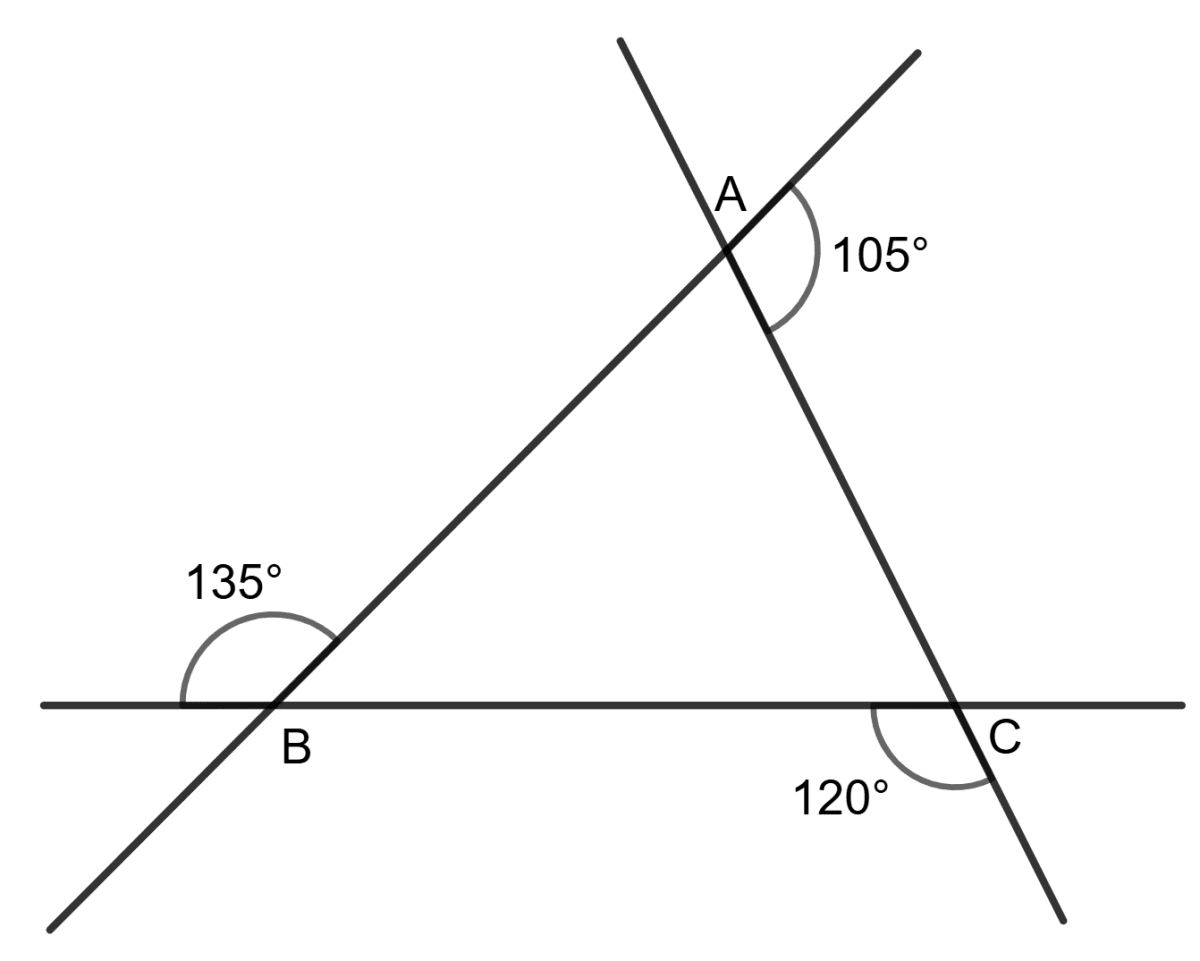
Reason (R): In △ABC,
∠BAC > ∠ACB > ∠ABC
⇒ BC > AB > AC
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Triangles
2 Likes
Answer
Both A and R are true.
Explanation
According to the rule that the sum of the angles in a linear pair is 180°:
∠ BAC + 105° = 180°
⇒ ∠ BAC = 180° - 105°
⇒ ∠ BAC = 75°
∠ ABC + 135° = 180°
⇒ ∠ ABC = 180° - 135°
⇒ ∠ ABC = 45°
∠ ACB + 120° = 180°
⇒ ∠ ACB = 180° - 120°
⇒ ∠ ACB = 60°
⇒ 75° > 60° > 45°
∠BAC > ∠ACB > ∠ABC
⇒ BC > AB > AC (side opposite to greater angle is greater)
∴ Assertion (A) is true.
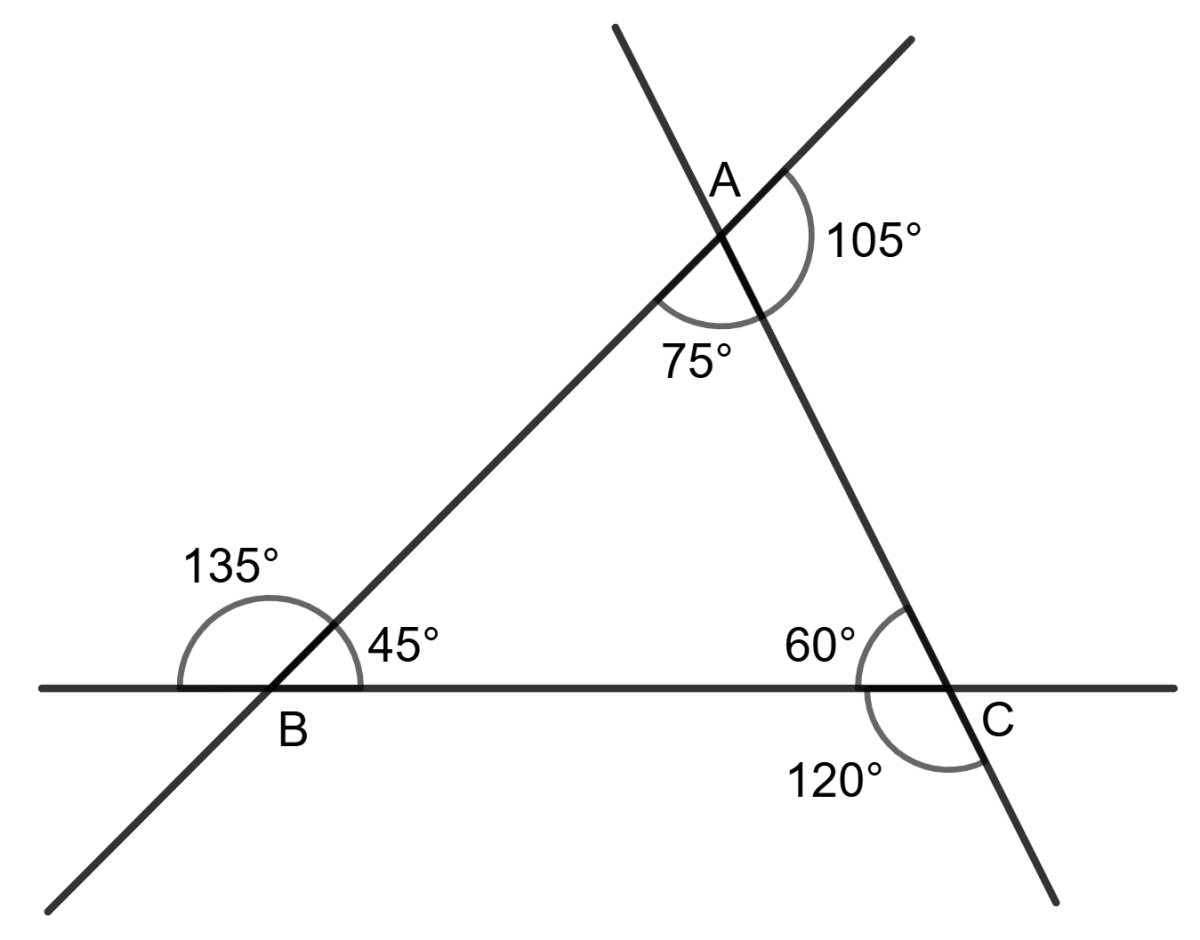
From the above calculations,
∠BAC > ∠ACB > ∠ABC
⇒ BC > AB > AC
∴ Reason (R) is true.
Hence, both Assertion (A) and Reason (R) are true.
Answered By
2 Likes
Related Questions
Assertion (A): Using the information in the given figure, we get : ∠PQR = ∠PSR = 90°
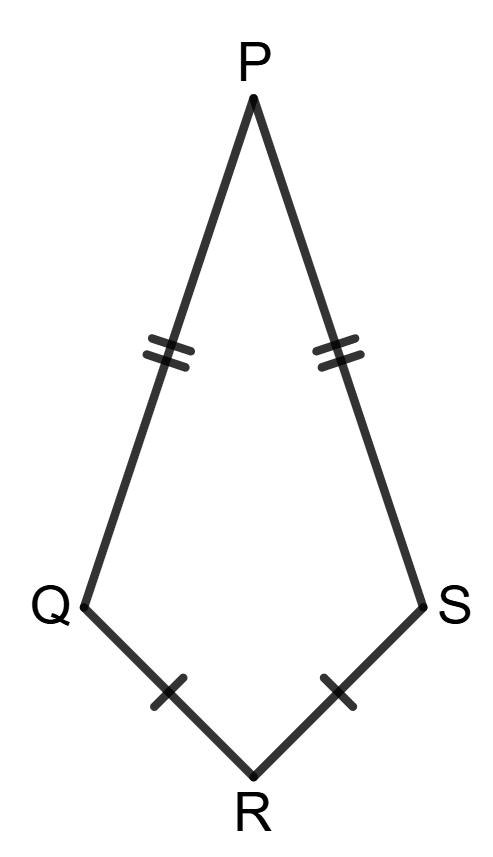
Reason (R):
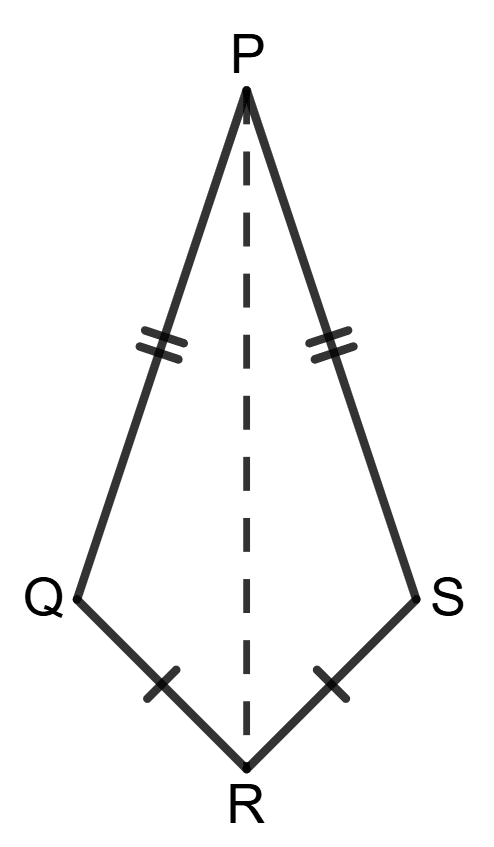
By SSS, △PQR = △PSR
⇒ ∠PQR = ∠PSR
Since, ∠PQR + ∠PSR ≠ 180°
∴ ∠PQR = ∠PSR ≠ 90°- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): A, B and C are three points. If AB = 8 cm, BC = 12 cm and AC = 25 cm. Points A, B and C do not form triangle ABC.
Reason (R):
AB + BC = 8cm + 12 cm = 20 cm
and AC = 25 cm
∴ AB + BC ≯ ACPoints A, B and C do not form triangle ABC.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Using the information in the given figure, we get CE : EA = 5:3.
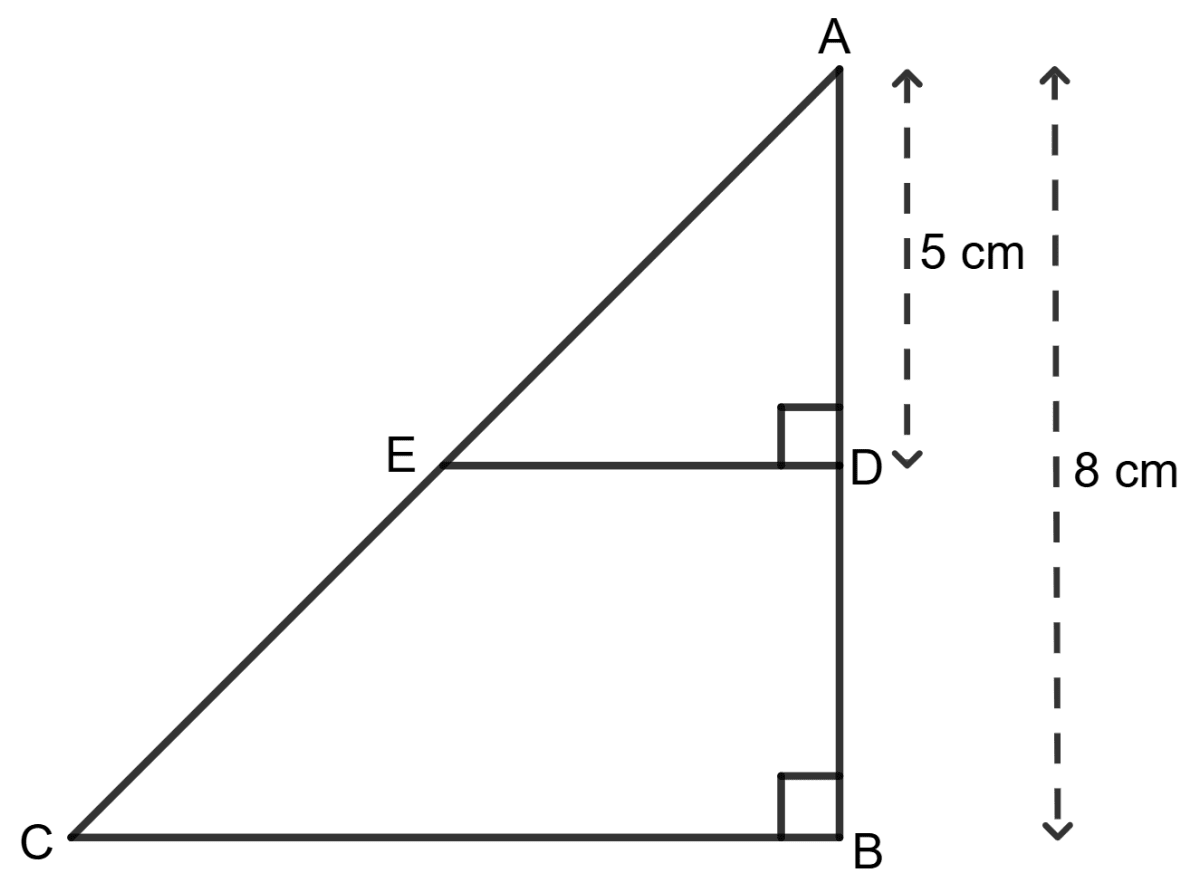
Reason (R): Since, ∠ADE = ∠ABC = 90°
so,
⇒ CE : EA = 3 : 5
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Using the information in the given figure, we have PQ = 10 cm.
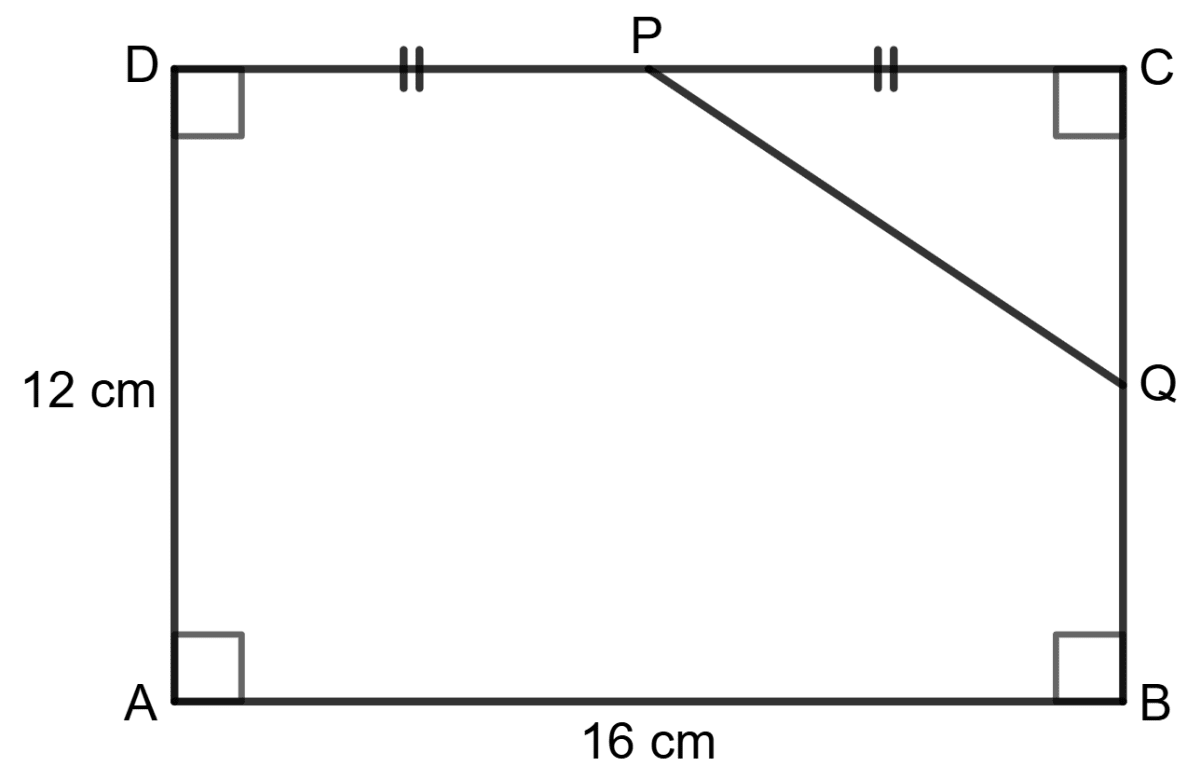
Reason (R): In right-triangle DAB, DB = 20 cm.

- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.