Mathematics
Assertion (A): If x = a cos θ + b sin θ and y = a cos θ - b sin θ, then x2 + y2 = a2 + b2
Reason (R): cos2θ + sin2θ = 1.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Trigonometrical Ratios
1 Like
Answer
Given, x = a cos θ + b sin θ and y = a cos θ - b sin θ
⇒ x2 = (a cos θ + b sin θ)2
⇒ x2 = a2 cos2 θ + b2 sin2 θ + 2 ab cos θ sin θ …………………(1)
Similarly,
⇒ y2 = (a cos θ - b sin θ)2
⇒ y2 = a2 cos2 θ + b2 sin2 θ - 2 a b cos θ sin θ …………………(2)
Adding equations (1) and (2), we get :
⇒ x2 + y2 = (a2 cos2 θ + b2 sin2 θ + 2ab cos θ sin θ) + (a2 cos2 θ + b2 sin2 θ - 2ab cos θ sin θ)
⇒ x2 + y2 = (a2 cos2 θ + a2 cos2 θ) + (b2 sin2 θ + b2 sin2 θ) + (2ab cos θ sin θ - 2ab cos θ sin θ)
⇒ x2 + y2 = 2a2 cos2 θ + 2 b2 sin2 θ
⇒ x2 + y2 = 2(a2 cos2 θ + b2 sin2 θ)
∴ Assertion (A) is false.
cos2 θ + sin2 θ = 1
This is a fundamental Pythagorean trigonometric identity and is always true for any real value of θ.
∴ Reason (R) is true.
∴ Assertion (A) is false, Reason (R) is true.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
Assertion (A): In the adjoining figure, tan A = . Then AC = 2AB.
Reason (R): In right angled ΔABC, AC2 = AB2 + BC2
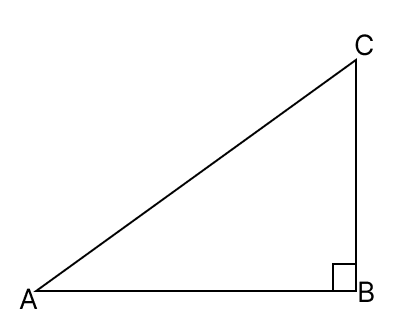
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Assertion (A): In adjoining triangle ABC, sinA cosA = .
Reason (R): cos A = .
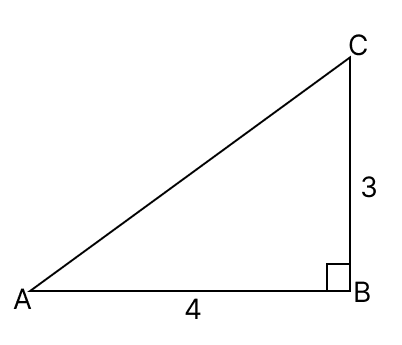
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
From the figure (i) given below, calculate all the six t-ratios for both acute angles.

From the figure (ii) given below, find the values of x and y in terms of t-ratios of θ.
