Mathematics
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Triangles
11 Likes
Answer
Triangle ABC with BE and CF as equal altitudes is shown in the figure below:
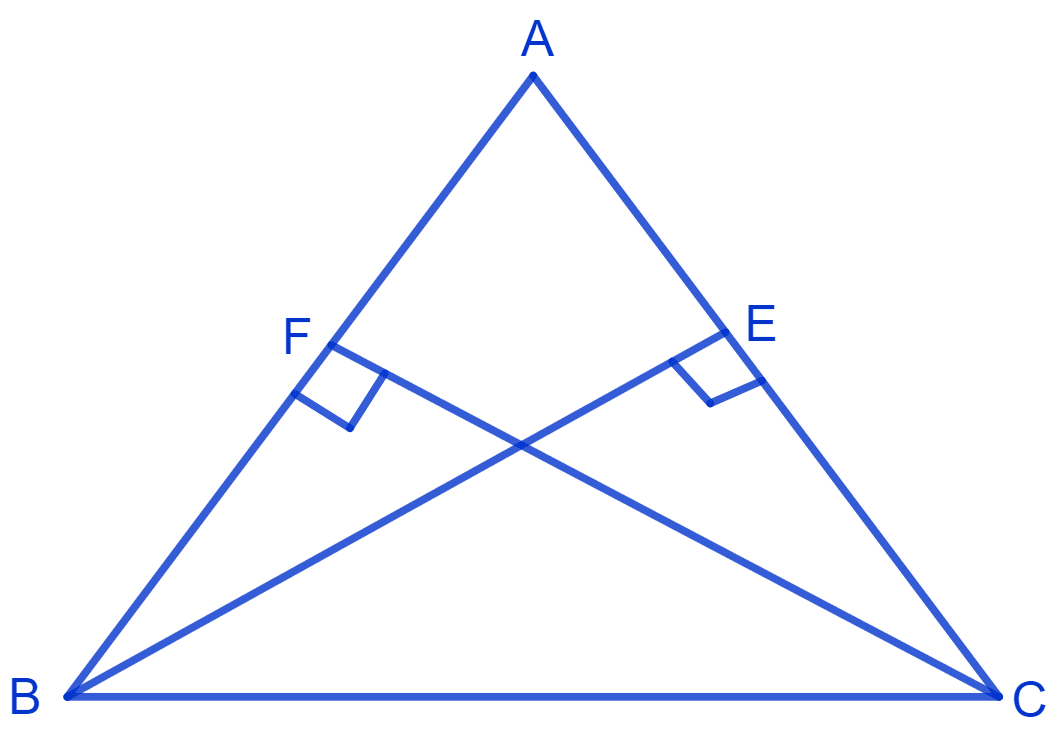
Given :
BE is a altitude.
∴ ∠AEB = ∠CEB = 90°
CF is a altitude.
∴ ∠AFC = ∠BFC = 90°
Also, BE = CF.
In Δ BEC and Δ CFB,
⇒ ∠BEC = ∠CFB (Each equal to 90°)
⇒ BC = CB (Common)
⇒ BE = CF (Given)
⇒ Δ BEC ≅ Δ CFB (By R.H.S. congruence rule)
We know that,
Corresponding parts of congruent triangle are equal.
⇒ ∠BCE = ∠CBF (By C.P.C.T.)
As,
Sides opposite to equal angles of a triangle are equal.
∴ AB = AC.
Hence, proved that Δ ABC is an isosceles triangle.
Answered By
7 Likes
Related Questions
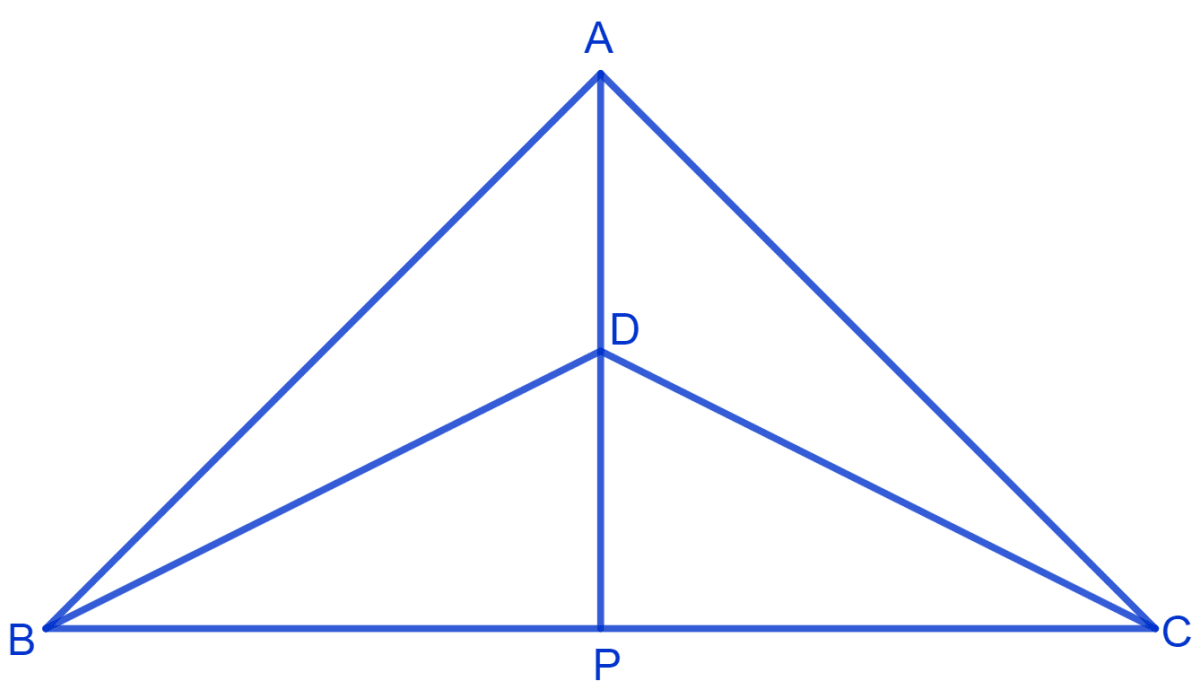
Δ ABC and Δ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that
(i) Δ ABD ≅ Δ ACD
(ii) Δ ABP ≅ Δ ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A
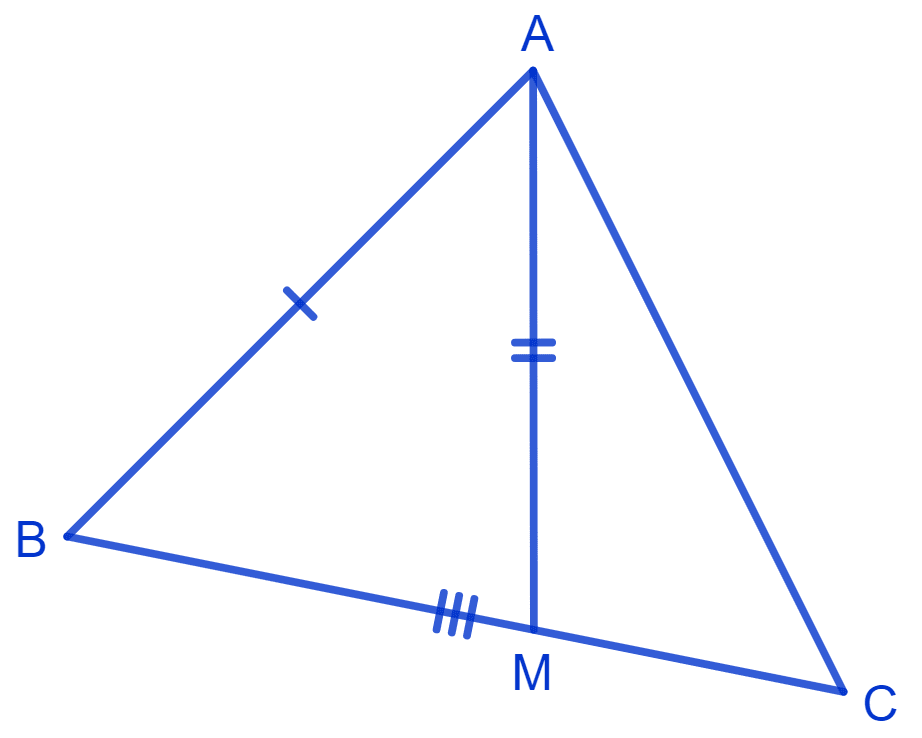
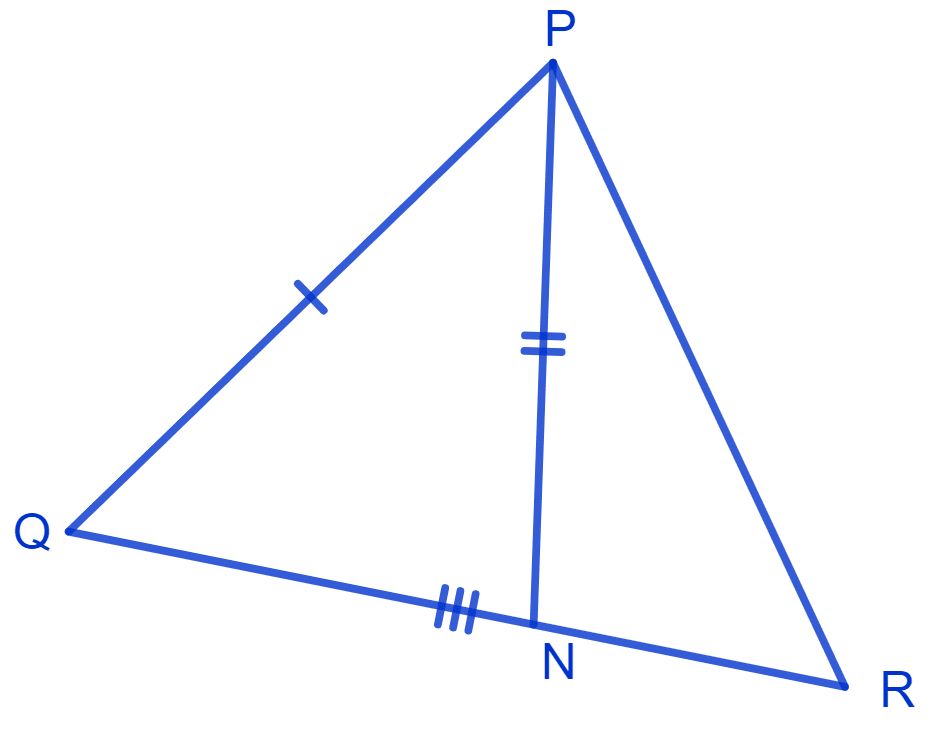
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of Δ PQR. Show that :
(i) Δ ABM ≅ Δ PQN
(ii) Δ ABC ≅ Δ PQR
ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.