Mathematics
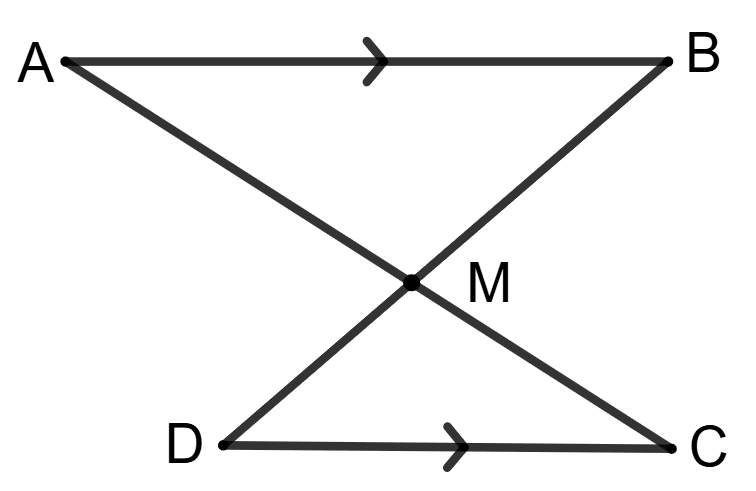
If BM = DM then AM = CM :
yes
no
can't say
none of these
Triangles
3 Likes
Answer
Given, BM = DM
⇒ M bisects line BD.
AB is parallel to CD.
In ΔABM and ΔCDM,
⇒ BM = DM
⇒ ∠MBA = ∠MDC (Alternate angles are equal)
⇒ ∠MAB = ∠MCD (Alternate angles are equal)
∴ ΔABM ≅ ΔCDM (By AAS congruency criterion)
By C.P.C.T.
⇒ AM = CM
Hence, option 1 is the correct option.
Answered By
1 Like
Related Questions
If two sides and an angle of one triangle are equal to two sides and an angle of the other triangle, then the triangle must be congruent
no
yes
can't say
If BA = DE, AC = DF and BF = EC, then the triangles ABC and DEF are congruent by axiom.
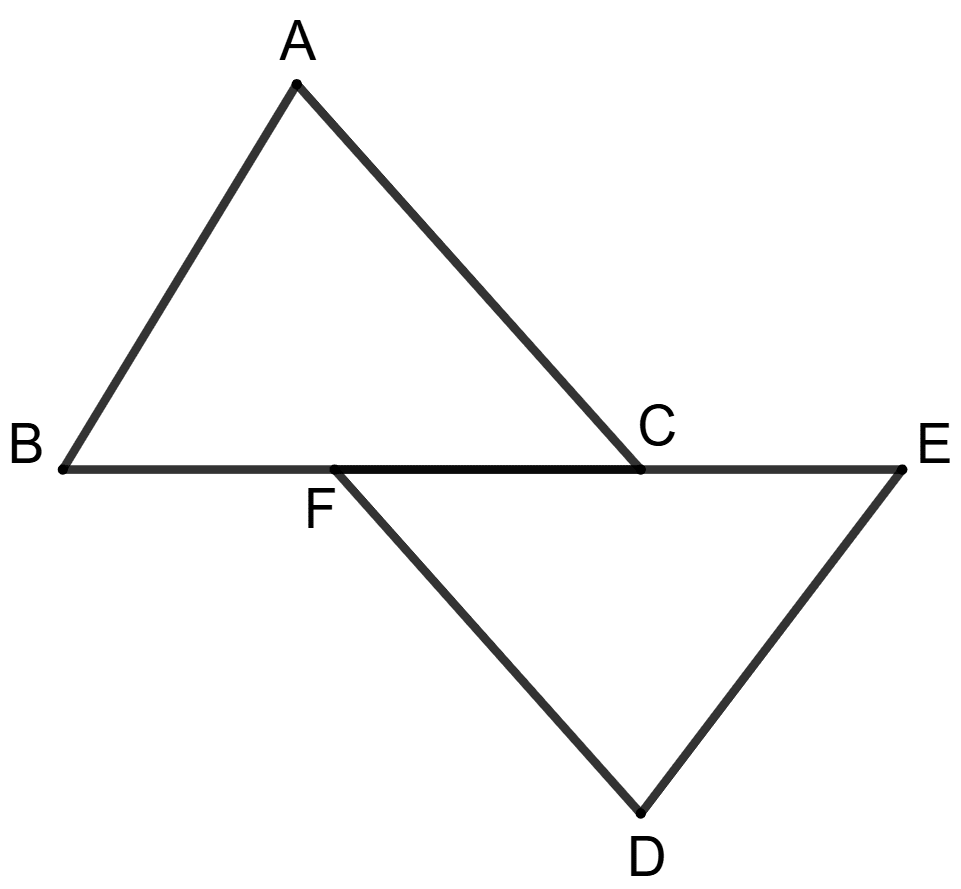
ASA
AAS
RHS
SSS
Statement 1: ∠A = ∠Q and ∠B = ∠R, then to get the triangles, congruent, we must have AB = PR.
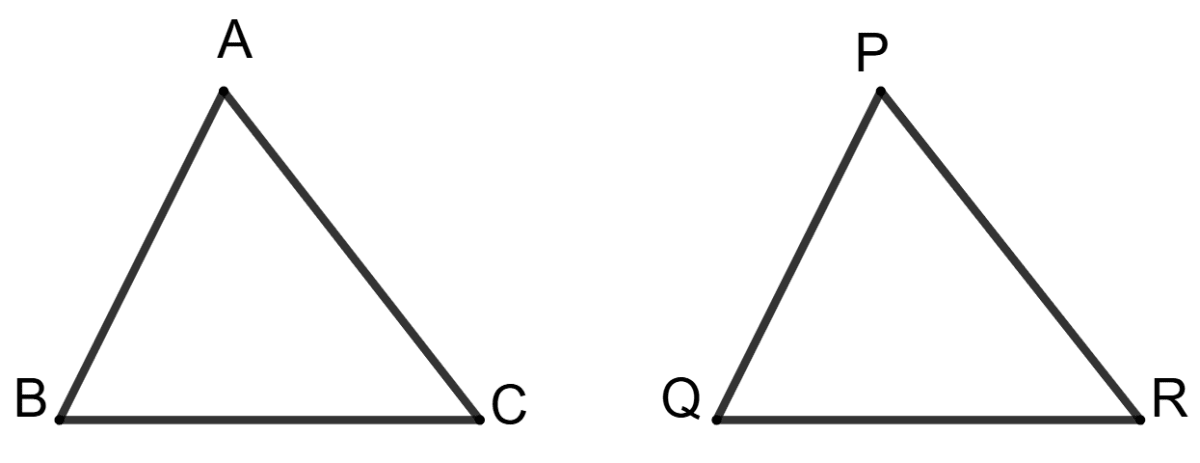
Statement 2: The given Δs will be congruent, if AB = QR.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Statement 1: MM' is a plane mirror and A is an object, then I is an image of object A.
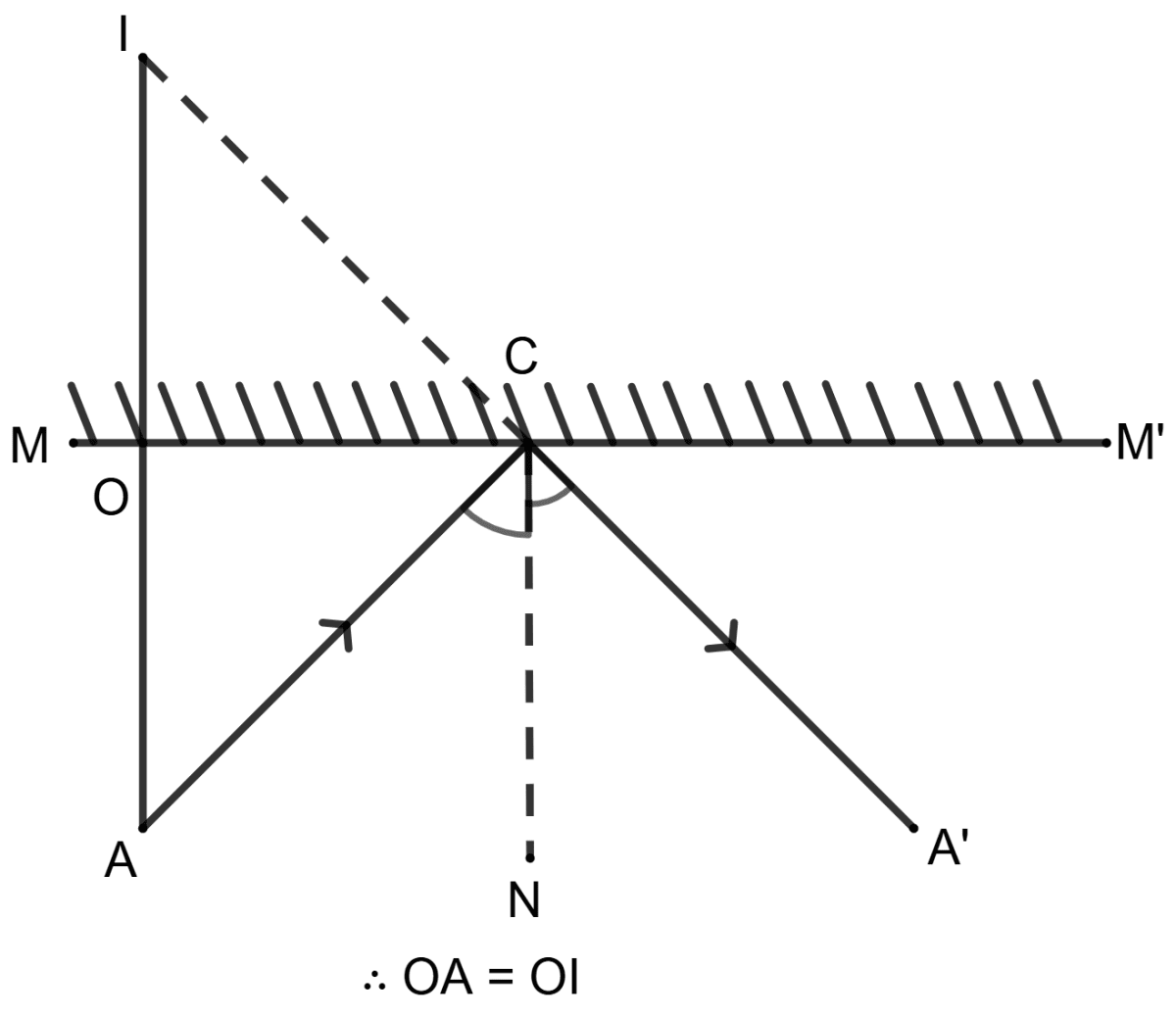
∴ OA = OI
Statement 2: ΔAOC ≅ ΔIOC by ASA. And, so CI = CA.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.