Mathematics
Statement 1: MM' is a plane mirror and A is an object, then I is an image of object A.
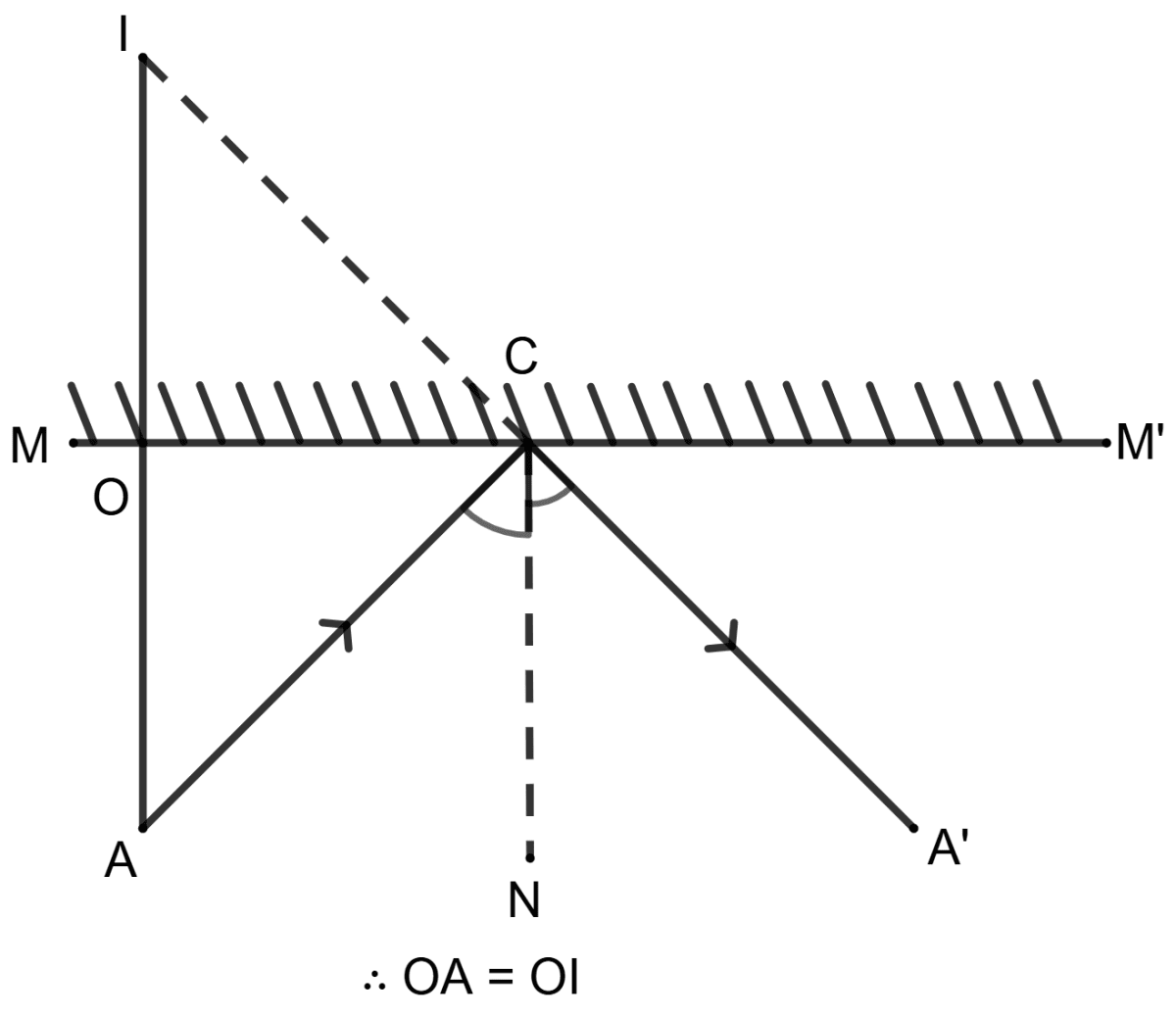
∴ OA = OI
Statement 2: ΔAOC ≅ ΔIOC by ASA. And, so CI = CA.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Triangles
2 Likes
Answer
Given, MM' is a plane mirror and A is an object, then I is an image of object A.
The image I of object A is located at the same distance behind the mirror as the object is in front of it, i.e. OA = OI.
So, statement 1 is true.
In ΔAOC and ΔIOC,
⇒ OA = OI (Proved above)
⇒ ∠AOC = ∠IOC (Both equal to 90°)
⇒ OC = OC (Common)
∴ ΔAOC ≅ ΔIOC (By ASA congruency criterion)
By C.P.C.T.C.,
⇒ CI = CA
So, statement 2 is true.
∴ Both the statements are true.
Hence, option 1 is the correct option.
Answered By
2 Likes
Related Questions
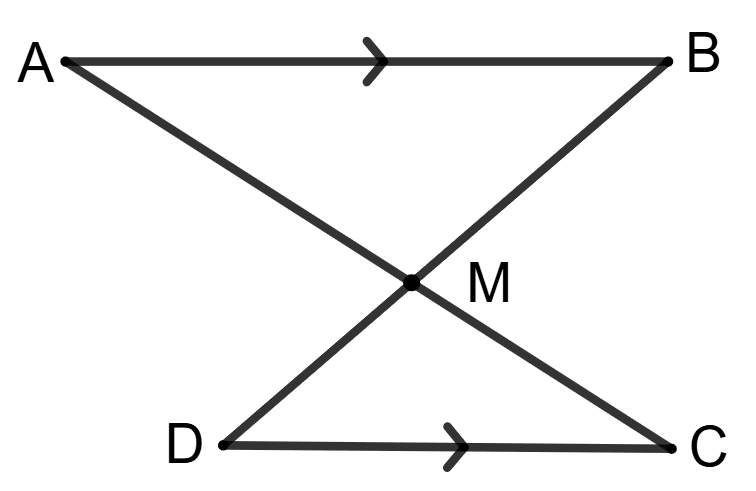
If BM = DM then AM = CM :
yes
no
can't say
none of these
Statement 1: ∠A = ∠Q and ∠B = ∠R, then to get the triangles, congruent, we must have AB = PR.
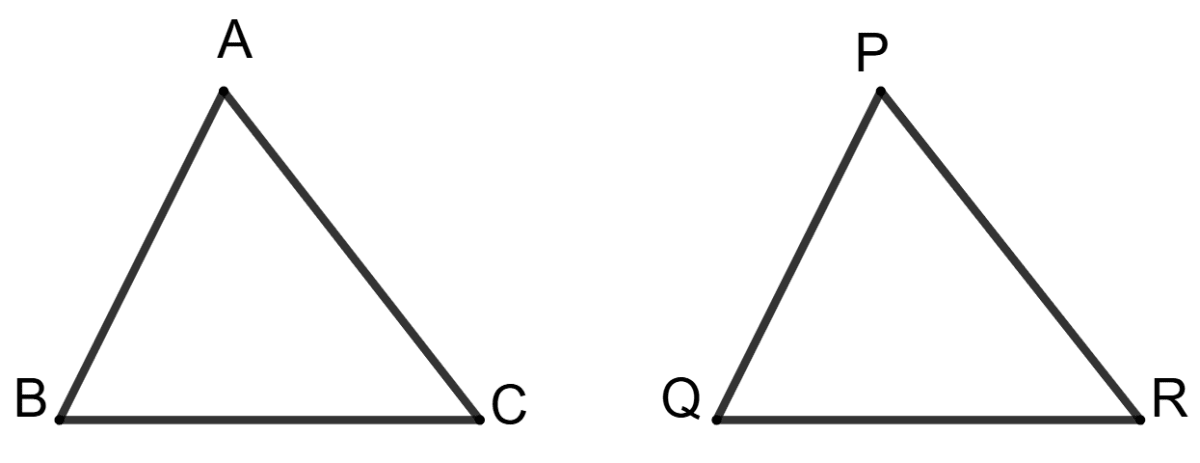
Statement 2: The given Δs will be congruent, if AB = QR.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Statement 1: If two angles and a side of one triangle are equal to two angles and a side of some another triangle, the triangles are congruent.
Statement 2: The two triangle will be congruent, if corresponding sides of the two triangles are equal.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): If PQ = PR, ΔPQS ≅ ΔPRT
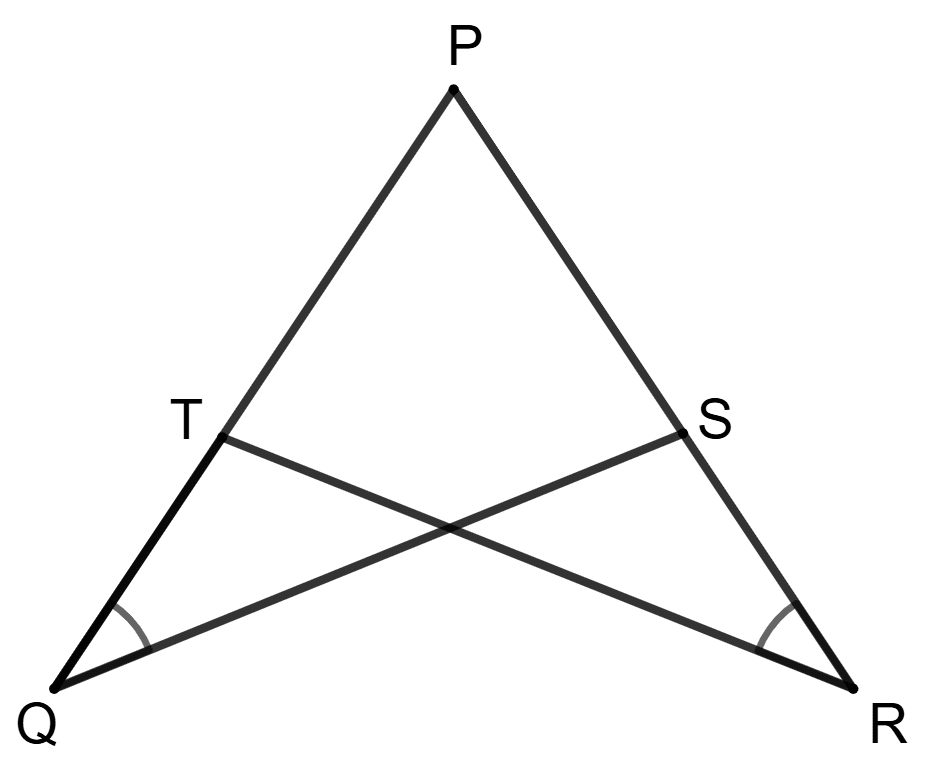
Reason (R): PQ = PR, ∠P = ∠P and ∠Q = ∠R
A is true, but R is false.
A is false, but R is true.
Both A and R are true and R is the correct reason for A.
Both A and R are true and R is the incorrect reason for A.