Mathematics
Statement 1: If two angles and a side of one triangle are equal to two angles and a side of some another triangle, the triangles are congruent.
Statement 2: The two triangle will be congruent, if corresponding sides of the two triangles are equal.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Triangles
1 Like
Answer
Given, statement "If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent."
The above statement is true and the triangles can be congruent by two axioms A.A.S. or A.S.A.
So, statement 1 is true.
Two triangles are congruent (by S.S.S. axiom) when all corresponding sides are equal in length, and all corresponding angles are equal in measure.
So, statement 2 is true.
Hence, option 1 is the correct option.
Answered By
1 Like
Related Questions
Statement 1: ∠A = ∠Q and ∠B = ∠R, then to get the triangles, congruent, we must have AB = PR.
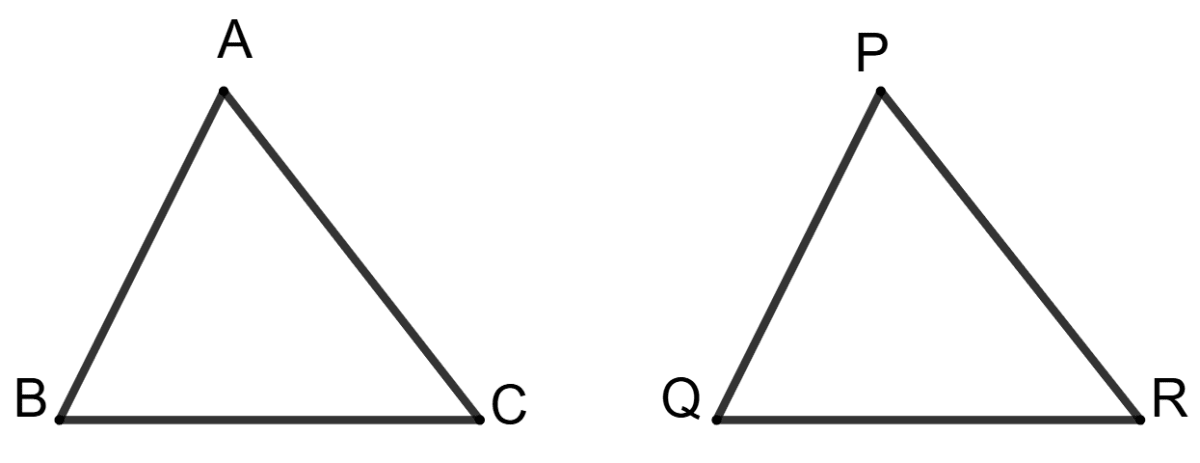
Statement 2: The given Δs will be congruent, if AB = QR.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Statement 1: MM' is a plane mirror and A is an object, then I is an image of object A.
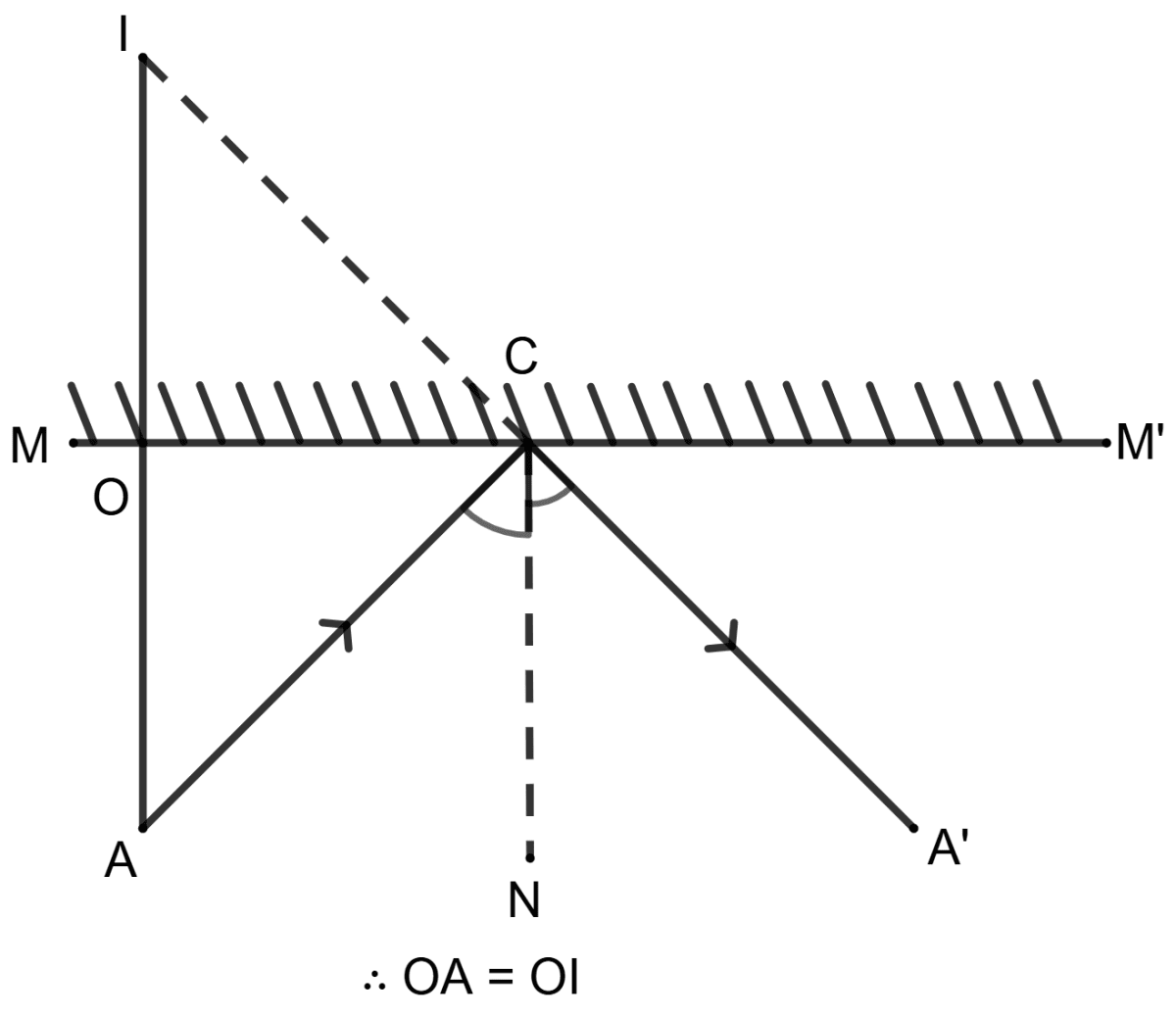
∴ OA = OI
Statement 2: ΔAOC ≅ ΔIOC by ASA. And, so CI = CA.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): If PQ = PR, ΔPQS ≅ ΔPRT
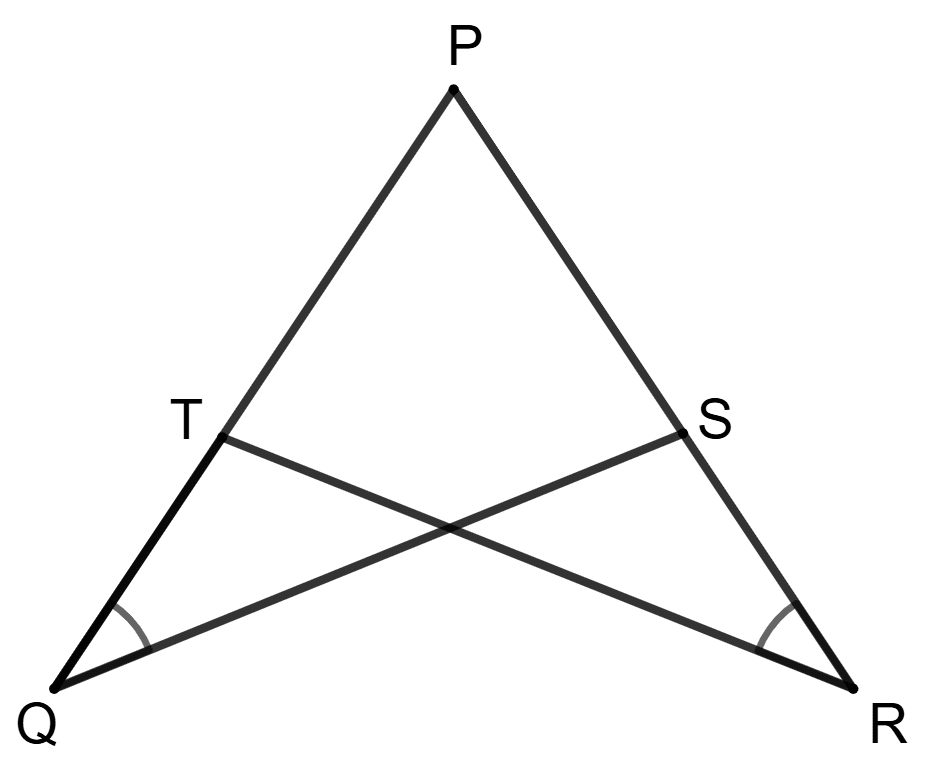
Reason (R): PQ = PR, ∠P = ∠P and ∠Q = ∠R
A is true, but R is false.
A is false, but R is true.
Both A and R are true and R is the correct reason for A.
Both A and R are true and R is the incorrect reason for A.
Assertion (A): ΔABD ≅ ΔACE
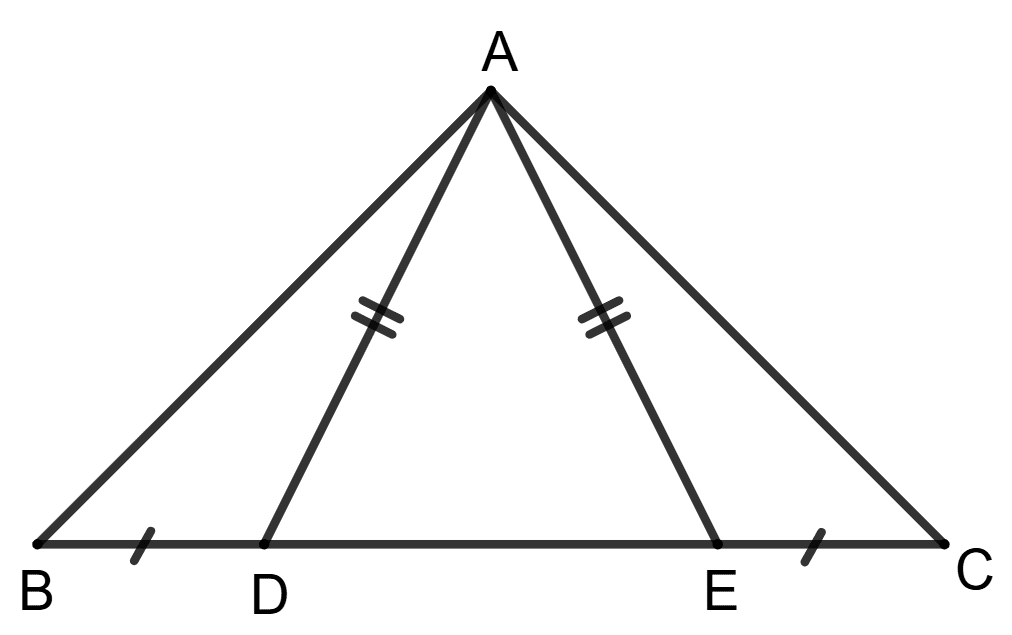
Reason (R): ∠ADE + ∠ADB = ∠AEC + ∠AED
But AD = AE
⇒ ∠ADE = ∠AED
∴ ∠ADB = ∠AEC
⇒ ∠ABD ≅ ∠AEC
A is true, but R is false.
A is false, but R is true.
Both A and R are true and R is the correct reason for A.
Both A and R are true and R is the incorrect reason for A.