Calculate the area of quadrilateral ABCD in which AB = 32 cm, AD = 24 cm, ∠A = 90° and BC = CD = 52 cm.

Quadrilateral ABCD is shown in the figure below:

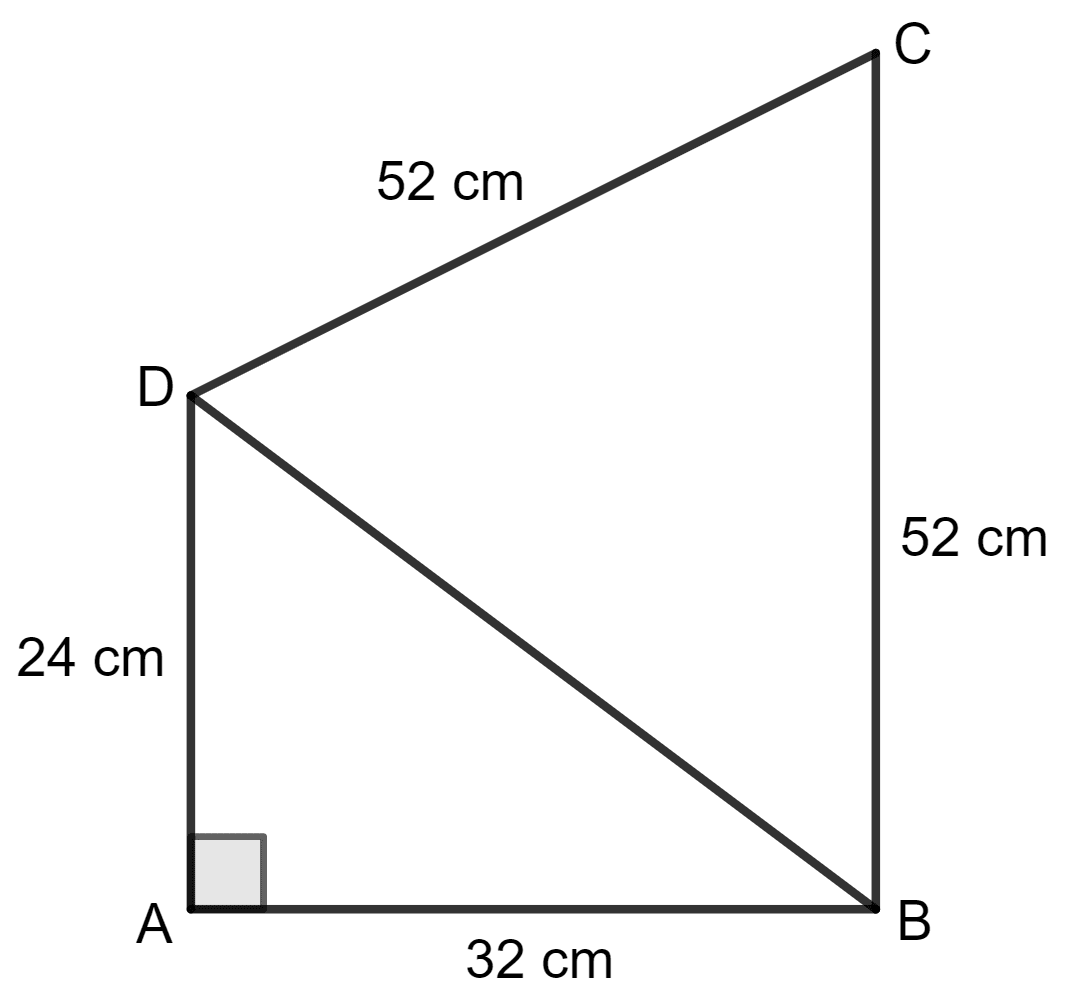
Area of Δ DAB = $\dfrac{1}{2}$ x base x height

= $\dfrac{1}{2}$ x DA x AB

= $\dfrac{1}{2}$ x 24 x 32 cm²

= 12 x 32 cm²

= 384 cm²

By using the Pythagoras theorem,

AD² + AB² = BD²

⇒ 24² + 32² = BD²

⇒ 576 + 1,024 = BD²

⇒ 1,600 = BD²

⇒ BD = $\sqrt{1,600}$

⇒ BD = 40 cm

In triangle BCD,

Let the sides of the triangle be:

a = 40 cm, b = 52 cm and c = 52 cm.

The semi-perimeter s:

$∵ s = \dfrac{a + b + c}{2}\\[1em] = \dfrac{40 + 52 + 52}{2}\\[1em] = \dfrac{144}{2}\\[1em] = 72$

∵ Area of Δ BCD = $\sqrt{s(s - a)(s - b)(s - c)}$

= $\sqrt{72(72 - 40)(72 - 52)(72 - 52)}$ cm²

= $\sqrt{72 \times 32 \times 20 \times 20}$ cm²

= $\sqrt{921,600}$ cm²

= 960 cm²

Therefore, area of quadrilateral ABCD = Area of Δ DAB + Area of triangle BCD

= 384 + 960 cm²

= 1344 cm²

Hence, the area of quadrilateral ABCD is 1344 cm².