Mathematics
Consider the following two statements:
Statement 1: The area of a square whose diagonal is 6 cm is 36 cm2.
Statement 2: A diagonal of a square divides it into two right angled isosceles triangle.
Which of the following is valid?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and Statement 2 is false.
Statement 1 is false, and Statement 2 is true.
Pythagoras Theorem
1 Like
Answer
Let's consider a square ABCD with diagonal AC.
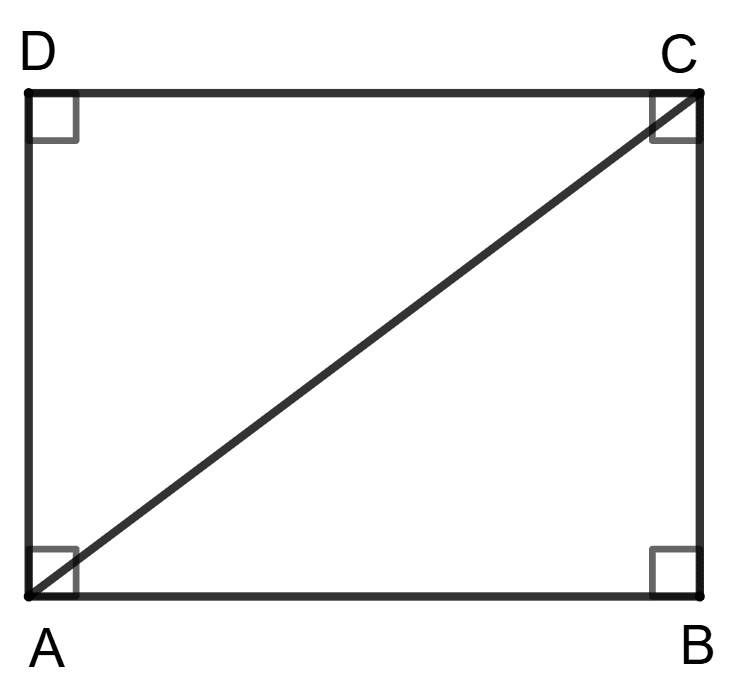
A square is a quadrilateral with four right angles.
Therefore, ∠A = ∠B = ∠C = ∠D = 90°.
AC divides the square into two triangles: △ABC and △ADC.
Both these triangles contain a right angle (at B and D respectively). Thus, they are right-angled triangles.
A square has all four sides equal in length. So, AB = BC = CD = DA.
In △ABC, the two sides AB and BC are equal (sides of the square).
In △ADC, the two sides AD and CD are equal (sides of the square).
Thus, AC divides the square into two right angled isosceles triangles.
∴ Statement 2 is true.
In triangle ABC,
By the Pythagorean theorem:
⇒ AC2 = AB2 + BC2
Let length of each side of square be a cm and length of diagonal equal to 6 cm (given).
⇒ 62 = a2 + a2
⇒ 36 = 2a2
⇒ a2 = = 18 cm2
As we know that area of square = a2
Thus, area = 18 cm2.
∴ Statement 1 is false.
∴ Statement 1 is false, and Statement 2 is true.
Hence, option 4 is the correct option.
Answered By
1 Like
Related Questions
A girl walks 200 m towards East and then she walks 150 m towards North. The distance of the girl from starting point is
350 m
250 m
300 m
225 m
A ladder reaches a window 12 m above the ground on one side of the street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 9 m high. If the length of the ladder is 15 m, then the width of the street is
30 m
24 m
21 m
18 m
Assertion (A): If the sides of a rectangular plot are 80 m and 60 m, then the length of its diagonal is 100 m.
Reason (R): In a rectangle, all angles are 90°.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Assertion (A): If triangle ABC is isosceles with AC = BC and AB2 = 2AC2, then triangle ABC is right angled.
Reason (R): If in a triangle ABC, we have AB2 = 2AC2 then we can conclude that it is right angled triangle.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).