Mathematics
Consider the following two statements:
Statement 1: In sin A = , then value of cot A is .
Statement 2: cot A = sin A.cos A.
Which of the following is valid?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and Statement 2 is false.
Statement 1 is false, and Statement 2 is true.
Trigonometrical Ratios
1 Like
Answer
Given, sin A =
By formula,
⇒ sin2 A + cos2 A = 1
⇒ + cos2 A = 1
⇒ + cos2 A = 1
⇒ cos2 A =
⇒ cos2 A =
⇒ cos A = .
By formula,
⇒ cot A = .
Thus, both the statements are false.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
If tan A = , then cos A is equal to
If sin θ = , then cos θ is equal to
Assertion (A): In the adjoining figure, tan A = . Then AC = 2AB.
Reason (R): In right angled ΔABC, AC2 = AB2 + BC2
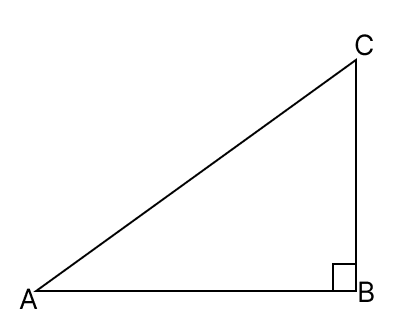
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Assertion (A): In adjoining triangle ABC, sinA cosA = .
Reason (R): cos A = .
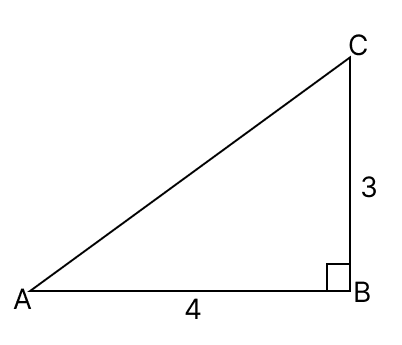
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).