Construct an angle ABC = 90°. Locate a point P which is 2.5 cm from AB and 3.2 cm from BC.

Steps:

1. Draw a line segment BC of any suitable length.

2. Taking B as centre, draw an arc of any suitable radius, which cuts BC at point E.

3. With E as centre and the same radius, as taken in step 2, draw an arc which cuts previous arc at point F.

4. With F as centre and the same radius, draw one more arc which cuts the first arc at point G.

5. With F and G as centres and radii equal to more than half the distance between F and G, draw arcs which cut each other at point H.

6. Join BH and produce upto any point A.
   ∠ABC so obtained is equal to 90° i.e., ∠ABC = 90°.

7. Taking any point Y on line BC and radii 3.2 cm, draw an arc.

8. Taking any point X on line AB and radii 2.5 cm, draw an arc which cut the arc drawn in step 7 at P.

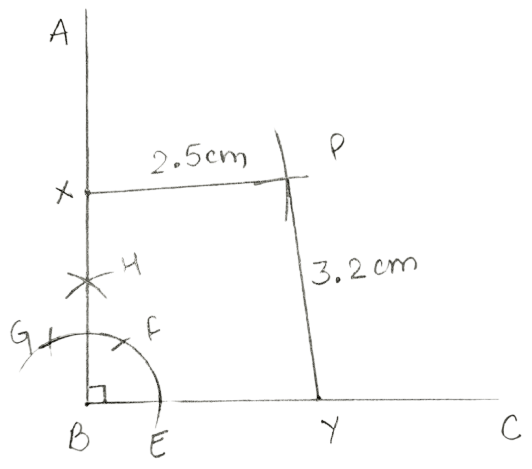
Hence, length of PX = 2.5 cm and PY = 3.2 cm.