Given below are the angles x, y and z.

Without measuring these angles construct :

(i) ∠ABC = x + y + z

(ii) ∠ABC = 2x + y + z

(iii) ∠ABC = x + 2y + z

(i) Steps:

1. Draw line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the angle x at the points Q and P, arms of the angle y at points S and R and arms of the angles z at points T and U.

3. From the arc, with centre B, cut MN = PQ = x, NO = SR = y and OX = TU = z.

4. Joint BX and produce upto point A.

Hence, ∠ ABC = x + y + z.

(ii) Steps:

1. Draw line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the angle x at the points P and Q, arms of the angles y at points R and S and arms of the angles z by at the points T and U.

3. From the arc, with centre B, cut MN = PQ = x, NO = PQ = x , OX = RS = y and XY = TU = z.

4. Joint BY and produce upto point A.

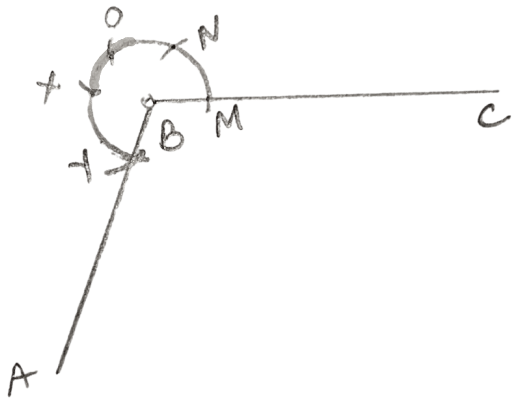
Hence, ∠ABC = 2x + y + z.

(iii) Steps:

1. Draw line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the angle x at the points P and Q, arms of the angle y at points R and S, and arms of the angle z at points T and U.

3. From the arc, with centre B, cut MN = PQ = x, NO = SR = y, OX = SR = y and XY = TU = z.

4. Joint BY and produce upto point A.

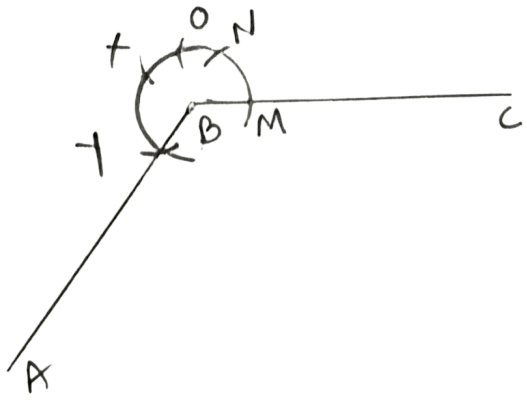
Hence, ∠ABC = x + 2y + z.