Mathematics
If each diagonal of a quadrilateral divides it into two triangles of equal areas, then prove that the quadrilateral is a parallelogram.
Theorems on Area
3 Likes
Answer
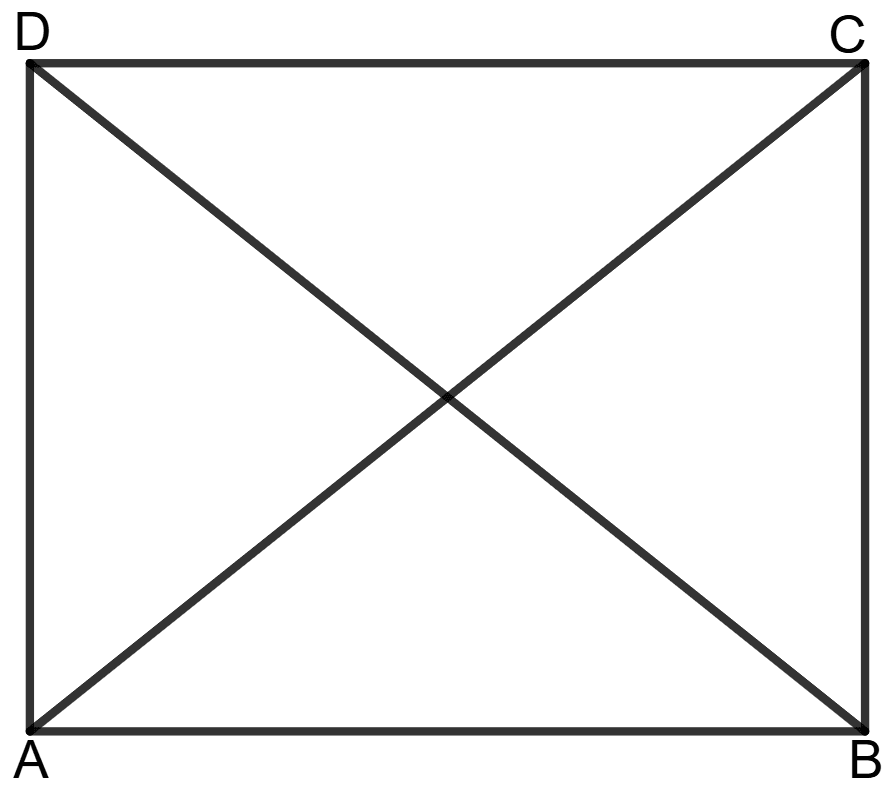
Given: ABCD is a quadrilateral where each diagonal divides it into two triangles of equal areas.
To prove: ABCD is a parallelogram.
Proof: Since each diagonal divides the quadrilateral into two triangles of equal areas, we have:
Area of Δ ABC = Area of ABCD ……………….(1)
Area of Δ ABD = Area of ABCD ……………….(2)
Area of Δ BCD = Area of ABCD ……………….(3)
From equations (1) and (2), we get:
Area of Δ ABC = Area of Δ ABD
Since Δ ABC and Δ ABD lie on same base AB and have equal areas, they must lie between the same parallel lines.
AB ∥ CD
Similarly, from equations (1) and (3), we get:
Area of Δ ABC = Area of Δ BCD
Since Δ ABC and Δ BCD lie on same base BC and have equal areas, they must lie between the same parallel lines.
BC ∥ AD
Since opposite sides are parallel, ABCD is a parallelogram.
Hence, ABCD is a parallelogram.
Answered By
1 Like
Related Questions
In the following figure, G is centroid of the triangle ABC.
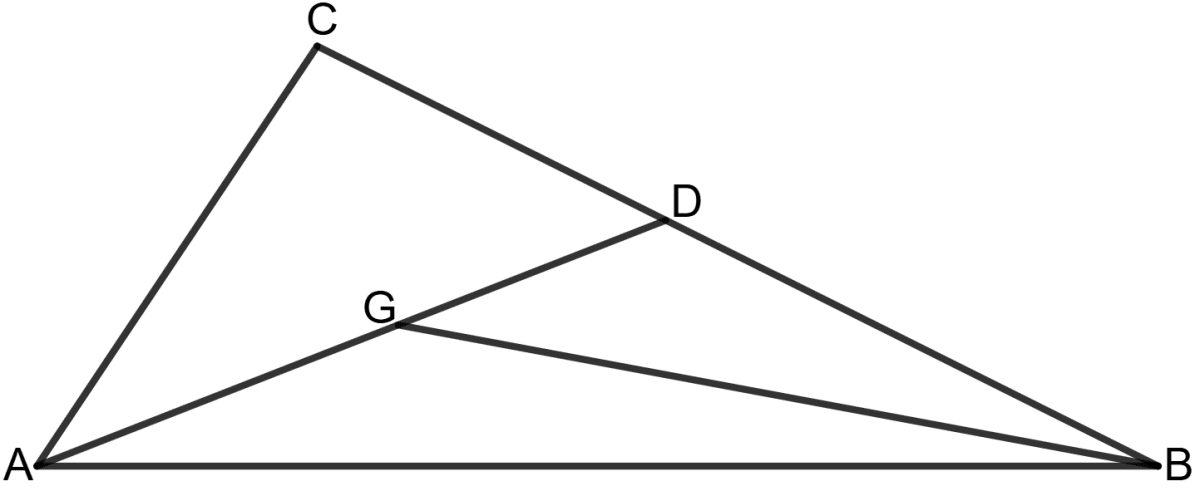
Prove that :
(i) Area (△ AGB) = x Area (△ ADB)
(ii) Area (△ AGB) = x Area (△ ABC)
Use the information given in the following figure to show that ar.(ABCQ) = ar.(ABCDE).
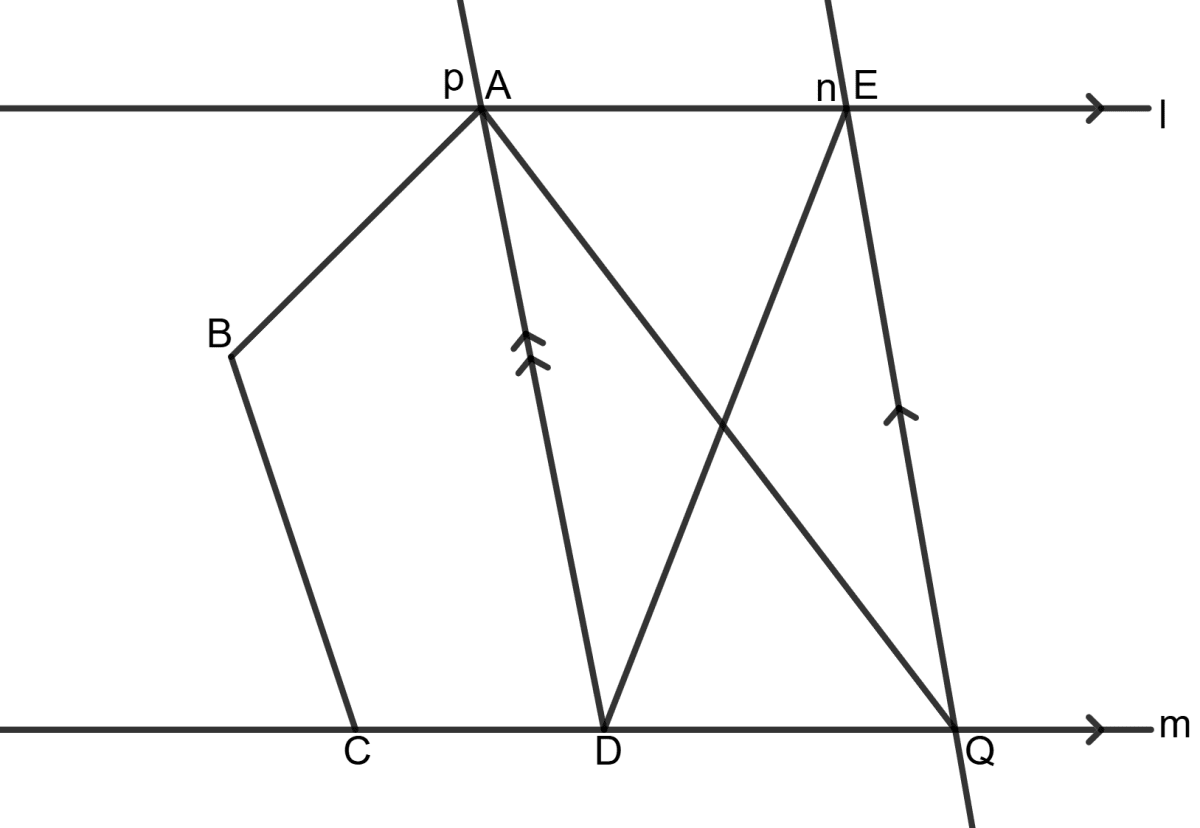
[Given : l // m and p // n]
In the given figure, ABCD, ABEF and AGHF are parallelograms.
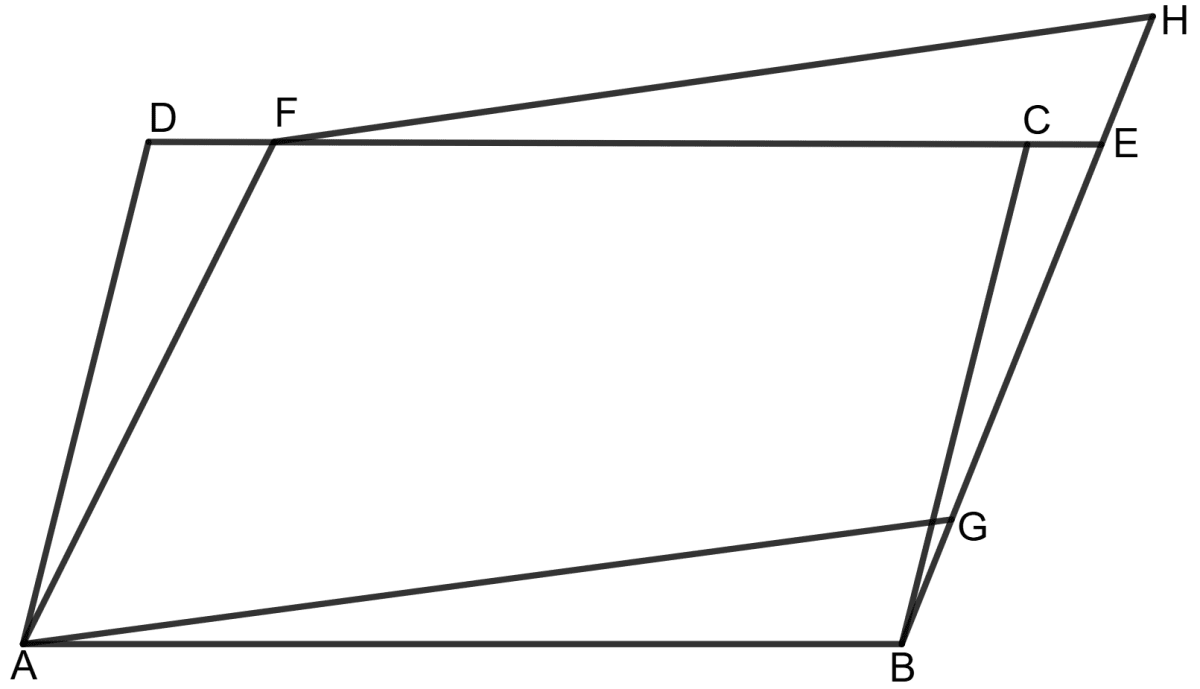
Prove that the area of parallelogram ABCD = area of parallelogram AGHF.
The area of the parallelogram ADFE is 275 cm2 and AD = 12.5 cm. Find the distance between point D and side EF.