Mathematics
In the following figure, G is centroid of the triangle ABC.
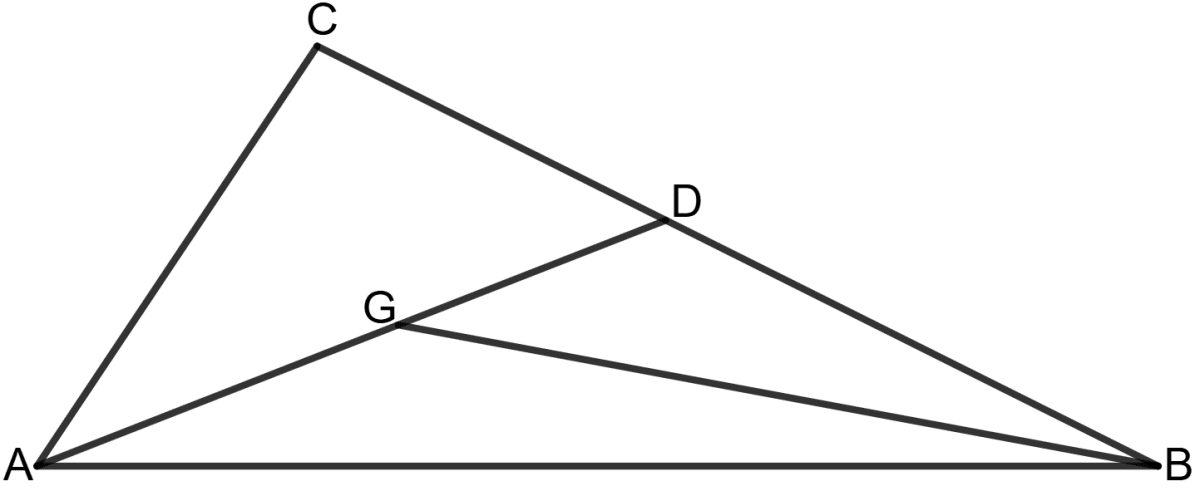
Prove that :
(i) Area (△ AGB) = x Area (△ ADB)
(ii) Area (△ AGB) = x Area (△ ABC)
Theorems on Area
2 Likes
Answer
(i) To Prove: Area (△ AGB) = x Area (△ ADB)
Proof: The centroid G of a triangle is the point of intersection of its three medians.
It divides each median into two segments, where the segment closer to the vertex is twice the length of the other.
If AD is a median, it divides △ ABC into two equal areas:
Area (△ ADB) = x Area (△ ABC)
Since G is the centroid, it divides △ ABC into three smaller triangles of equal area.
Area (△ AGB) = x Area (△ ABC)
=
Hence, Area (△ AGB) = x Area (△ ADB).
(ii) As proved above,
Area (△ AGB) = x Area (△ ABC)
Hence, Area (△ AGB) = x Area (△ ABC).
Answered By
3 Likes
Related Questions
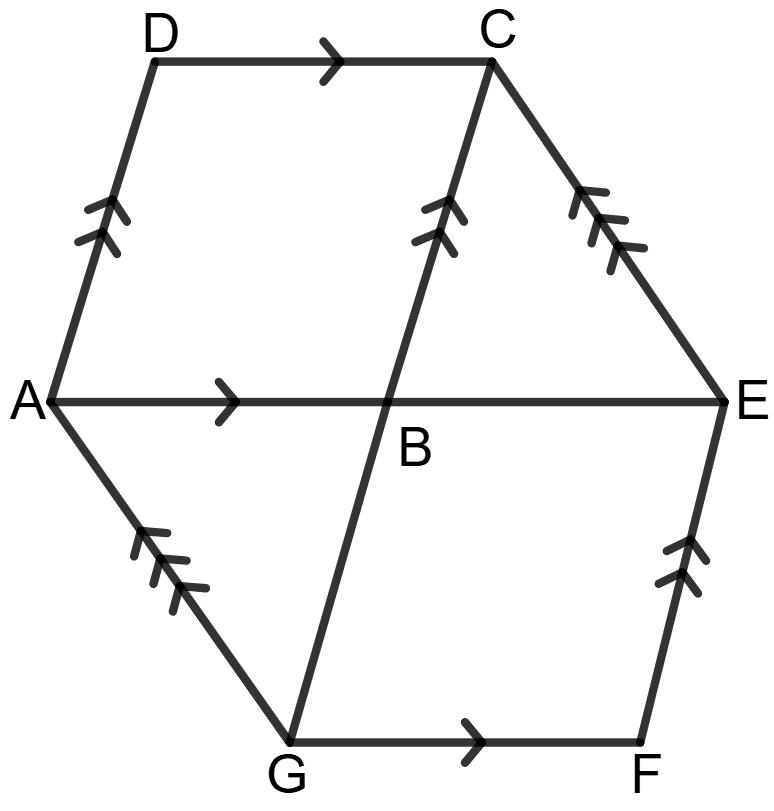
The following diagram shows two parallelograms ABCD and BEFG.
Prove that :
Area of // gm ABCD = Area of // gm BEFG.
In the parallelogram ABCD, the side AB is produced to the point X, so that BX = AB. The line DX cuts BC at E. Prove that
(i) DBXC is a parallelogram.
(ii) Area (△ AED) = 2 x area (△ CEX).
Use the information given in the following figure to show that ar.(ABCQ) = ar.(ABCDE).
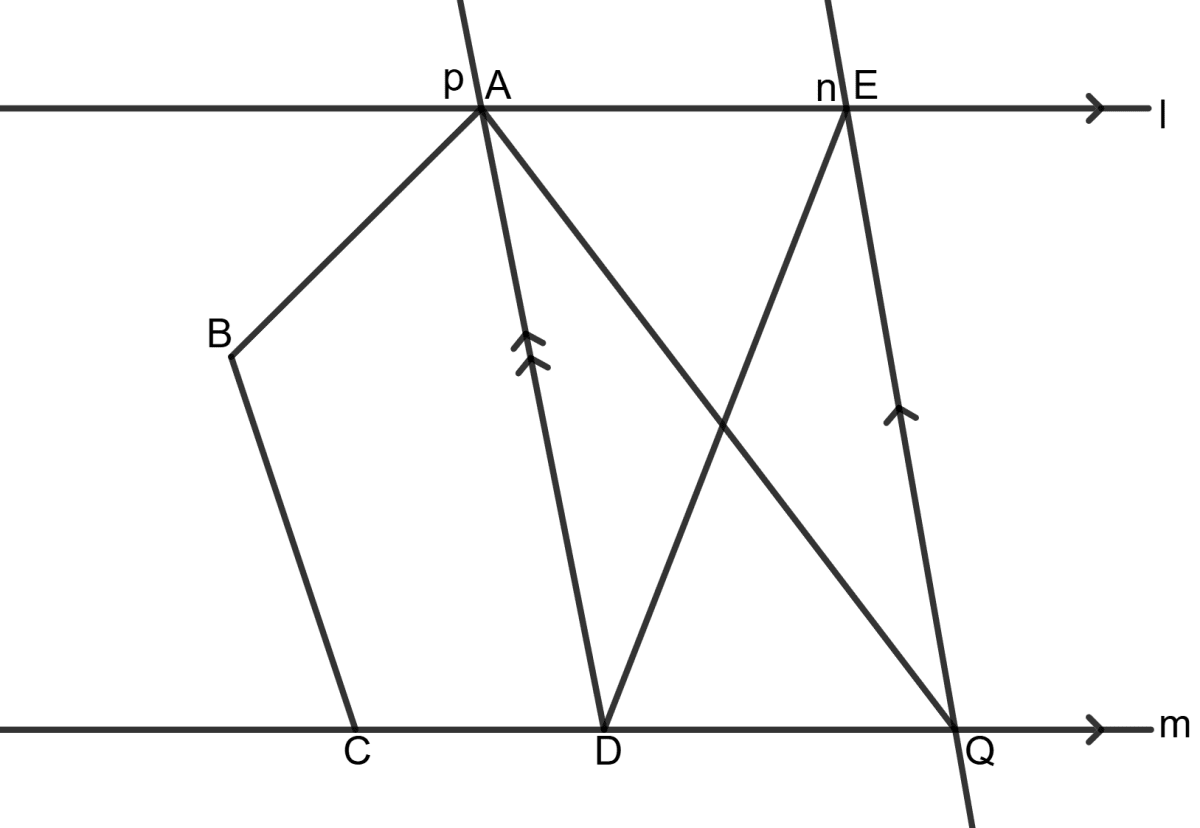
[Given : l // m and p // n]
If each diagonal of a quadrilateral divides it into two triangles of equal areas, then prove that the quadrilateral is a parallelogram.