Mathematics
In the parallelogram ABCD, the side AB is produced to the point X, so that BX = AB. The line DX cuts BC at E. Prove that
(i) DBXC is a parallelogram.
(ii) Area (△ AED) = 2 x area (△ CEX).
Theorems on Area
4 Likes
Answer
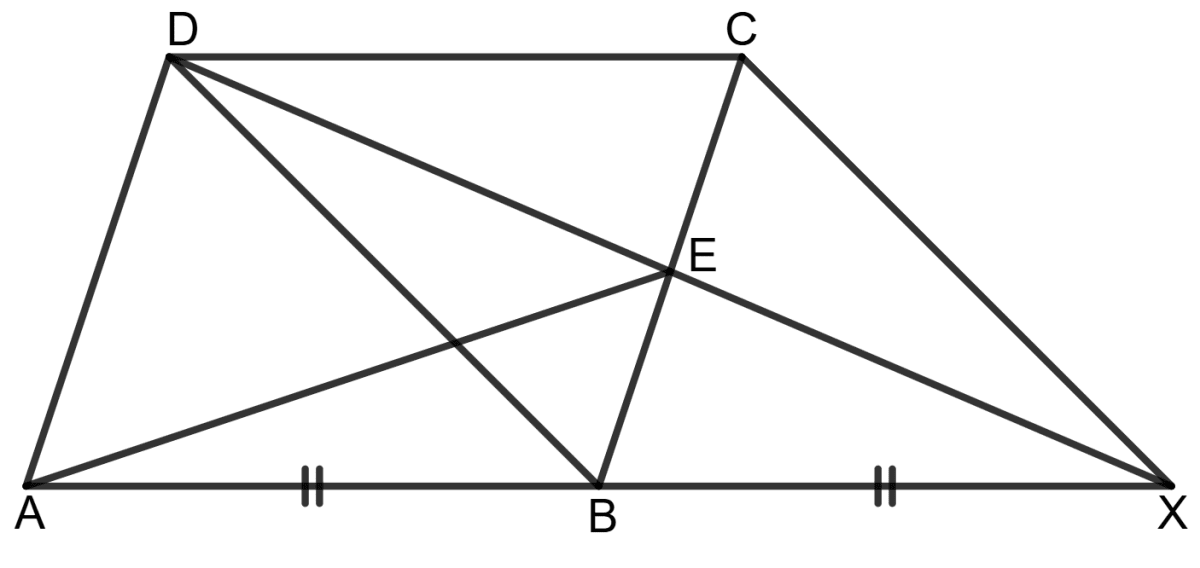
(i) Given: ABCD is a parallelogram, the side AB is extended to the point X such that BX = AB.
The line DX cuts BC at E.
To prove: DBXC is a parallelogram.
Proof: Since ABCD is a parallelogram, we know that:
AB = DC and AB ∥ DC
Given that AB = BX, we get:
⇒ DC = BX and DC ∥ BX
Since one pair of opposite sides of quadrilateral DBXC is both equal and parallel, it follows that:
Hence, DBXC is a parallelogram.
(ii) Given: From part (i), DBXC is a parallelogram, which implies that E is the midpoint of parallelogram DBXC.
To prove: Area (△ AED) = 2 x area (△ CEX)
Proof: Since E is the midpoint of parallelogram DBXC, the line AE acts as a median in Δ ADX, dividing it into two equal areas:
ar.(Δ AED) = ar.(Δ AEX) ……………….(1)
Similarly, BE is a median in Δ AED, dividing Δ AEX into two equal triangles:
ar.(Δ AEB) = ar.(Δ BEX) = ar.(Δ AEX) ……………….(2)
Since XE is a median in Δ BXC, it divides it into two equal areas:
ar.(Δ CEX) = ar.(Δ BEX)
Substituting equation (2), we get:
ar.(Δ CEX) = ar.(Δ AEX)
Since from equation (1), ar.(Δ AEX) = ar.(Δ AED), we can write:
ar.(Δ CEX) = ar.(Δ AED)
So, ar.(Δ AED) = 2 x ar.(Δ CEX)
Hence, ar.(Δ AED) = 2 x ar.(Δ CEX).
Answered By
4 Likes
Related Questions
Construct a rectangle ABCD with diagonal AC = 6.6 cm, side BC = 5.2 cm and ∠B = 90°.
The following diagram shows two parallelograms ABCD and BEFG.
Prove that :
Area of // gm ABCD = Area of // gm BEFG.
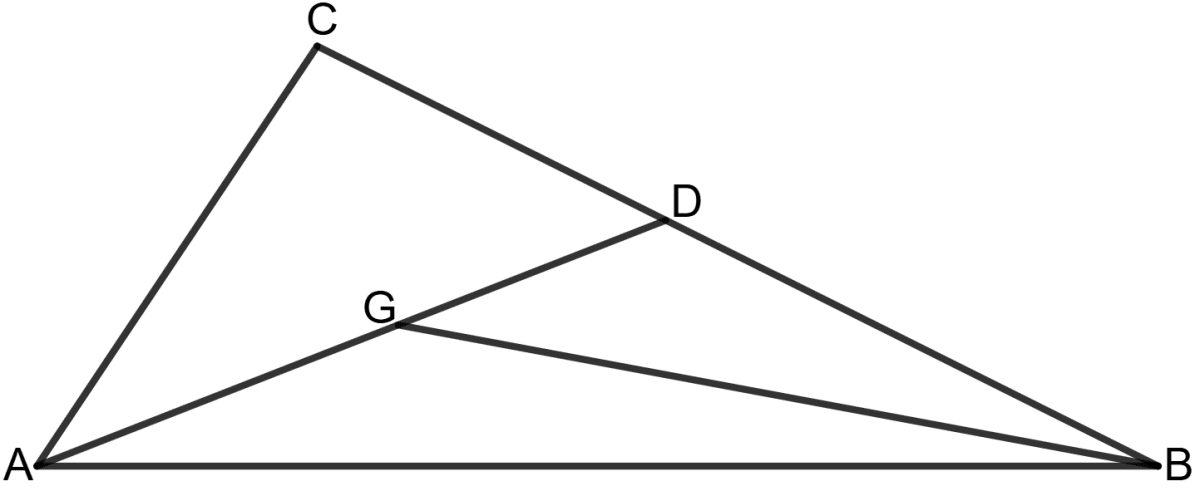
In the following figure, G is centroid of the triangle ABC.
Prove that :
(i) Area (△ AGB) = x Area (△ ADB)
(ii) Area (△ AGB) = x Area (△ ABC)
Use the information given in the following figure to show that ar.(ABCQ) = ar.(ABCDE).
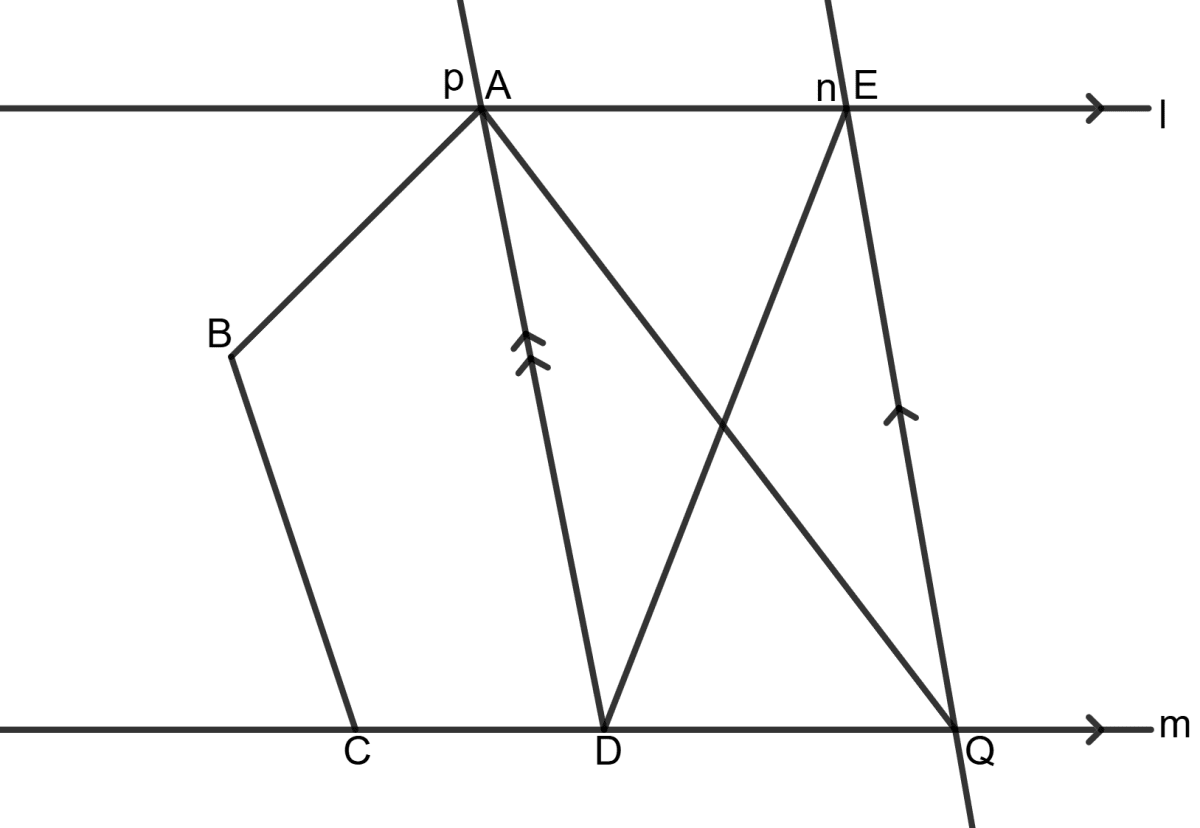
[Given : l // m and p // n]