Mathematics
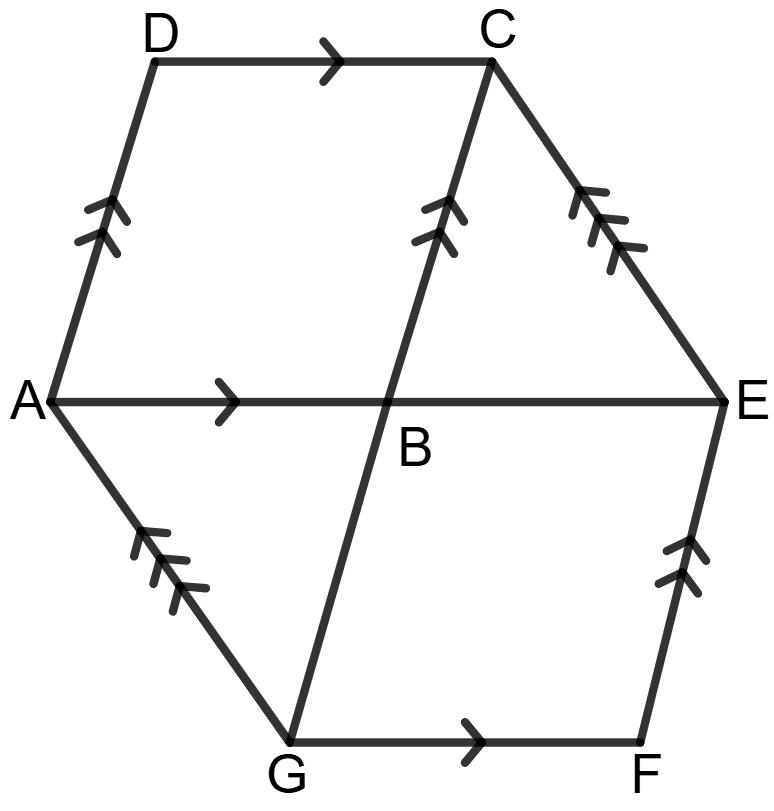
The following diagram shows two parallelograms ABCD and BEFG.
Prove that :
Area of // gm ABCD = Area of // gm BEFG.
Theorems on Area
3 Likes
Answer
Given: ABCD and BEFG are two parallelograms.
To prove: Area of // gm ABCD = Area of // gm BEFG
Construction: Join AC and GE.
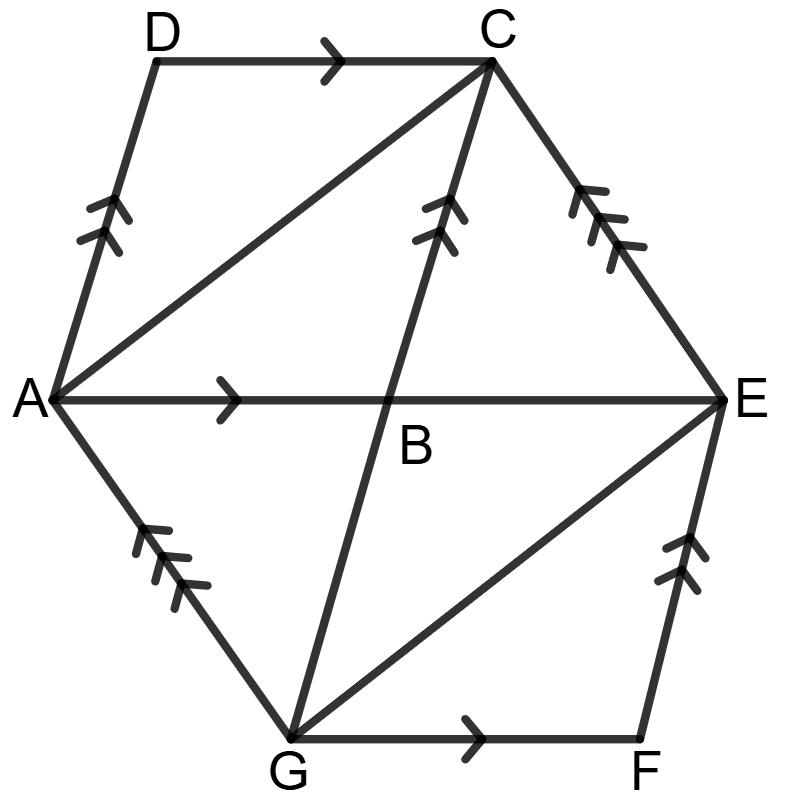
Proof: We know that if two triangles have the same base and height, their areas will be equal.
Since AG is a common base,
Area (Δ ACG) = Area (Δ AEG)
Adding Area (Δ ABG) on both sides,
⇒ ar.(Δ ABC) + ar.(Δ ABG) = ar.(Δ ABG) + ar.(Δ BGE)
⇒ ar.(Δ ABC) = ar.(Δ BGE) ……………….(1)
Since the area of a triangle is always half the area of a parallelogram when they share the same base and height, we can write:
ar.(Δ ABC) = ar.(∥gm ABCD)
ar.(Δ BGE) = ar.(∥gm BEFG)
From equation (1),
⇒ ar.(∥gm ABCD) = ar.(∥gm BEFG)
⇒ ar.(∥gm ABCD) = ar.(∥gm BEFG)
Hence, Area of // gm ABCD = Area of // gm BEFG.
Answered By
2 Likes
Related Questions
Construct a rhombus ABCD in which AC = 5.6 cm and BD = 6.3 cm
Construct a rectangle ABCD with diagonal AC = 6.6 cm, side BC = 5.2 cm and ∠B = 90°.
In the parallelogram ABCD, the side AB is produced to the point X, so that BX = AB. The line DX cuts BC at E. Prove that
(i) DBXC is a parallelogram.
(ii) Area (△ AED) = 2 x area (△ CEX).
In the following figure, G is centroid of the triangle ABC.
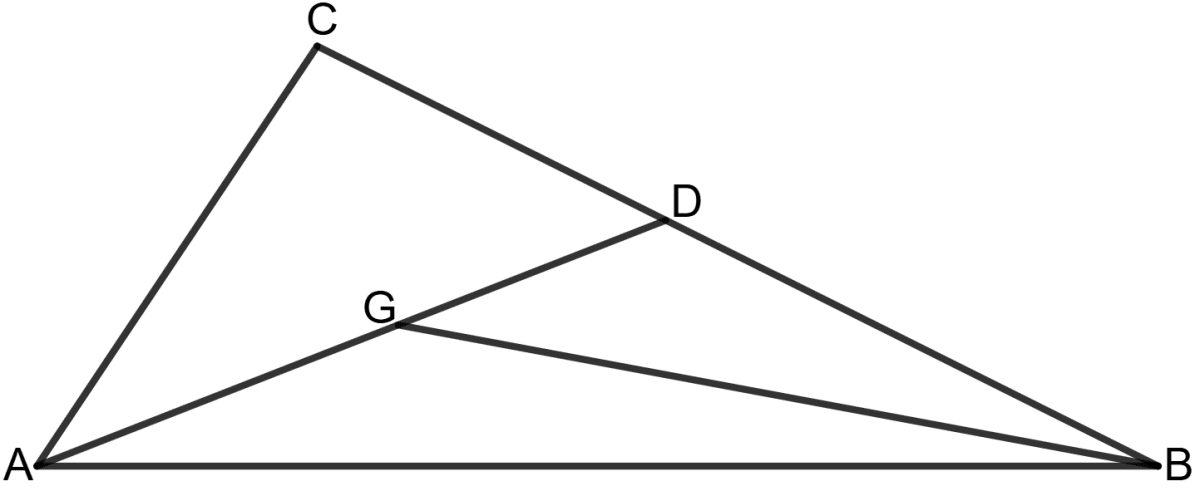
Prove that :
(i) Area (△ AGB) = x Area (△ ADB)
(ii) Area (△ AGB) = x Area (△ ABC)