Physics
The diagram below shows a fish in the tank and its image seen in the surface of water.

(a) Name the phenomenon responsible for the formation of this image.
(b) A double convex lens with refractive index μ1 inside two liquids of refractive indices μ2 and μ3 are shown in the diagrams below. The refractive indices are such that μ2 > μ1 and μ1 > μ3

How would a parallel incident beam of light refract when it comes out of the lens in each of the cases shown above?
(1) in figure a.
(2) in figure b.
Refraction Plane Surfaces
15 Likes
Answer
(a) Total internal reflection.
(b) According to the lens maker formula :
……(i)
(1) In figure a :
Refractive index of 1st medium = μ3
Refractive index of 2nd medium = μ1
Then ,from relation (i)
As,
μ1 > μ3
Since, the resulting focal length is positive so this lens behaves as a converging lens.
Hence, a parallel incident beam of light converges when it comes out of the lens im figure a.
(2) In figure b :
Refractive index of 1st medium = μ2
Refractive index of 2nd medium = μ1
Then, from relation (i)
As,
μ1 < μ2
Since, the resulting focal length is negative so this lens behaves as a diverging lens.
Hence, a parallel incident beam of light diverges when it comes out of the lens im figure b.
Answered By
9 Likes
Related Questions
(a) Name the radiations that are emitted during the decay of a nucleus, which has highest penetrating power?
(b) Does the emission of the above-mentioned radiation result in a change in the mass number?
The graph (fig A) illustrates the correlation between the number of protons (x-axis) and the number of neutrons (y-axis) for elements A, В, C, D, and E in the periodic table. These elements are denoted by the letters rather than their conventional symbols. When the element C, depicted in the graph, undergoes radioactive decay, it releases radioactive rays. When these rays are directed into the plane of the paper in the presence of a magnetic field, as indicated in the fig B, they experience deflection, causing them to move upwards.
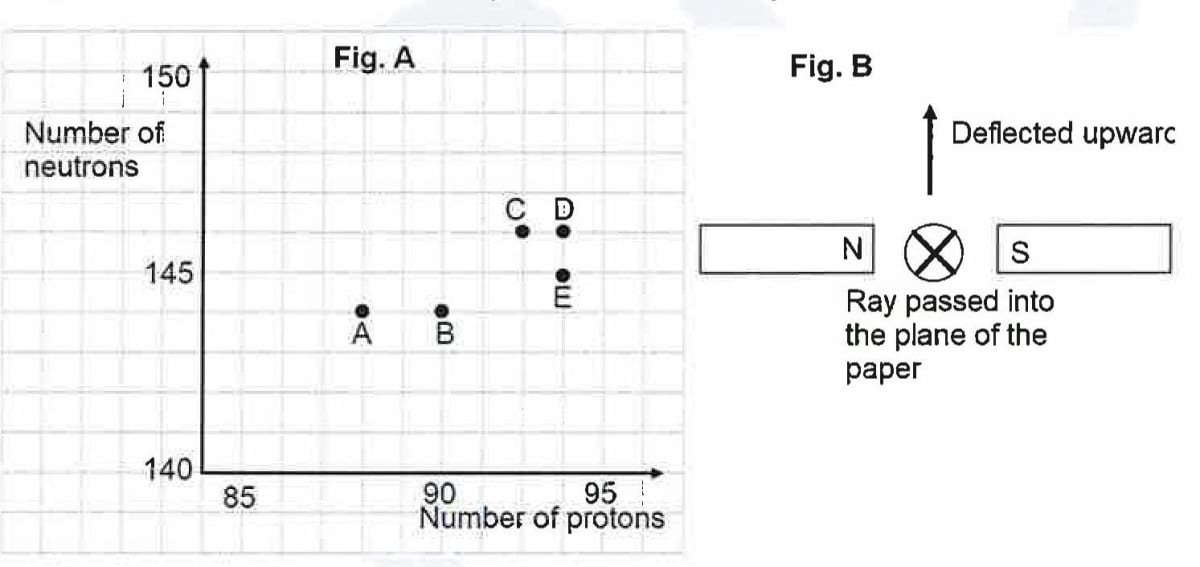
(a) Name the radioactive radiations emitted by the element C.
(b) Identify the daughter element from the graph.
(c) Name the law used to identify the radioactive radiations emitted by the element.
The refractive index of water is 1.33 at a certain temperature. When the temperature of water is increased by 40°C, the refractive index changes to 'x'.
(a) State whether x < 1.33 or x > 1.33.
(b) State two differences between normal reflection and total internal reflection.
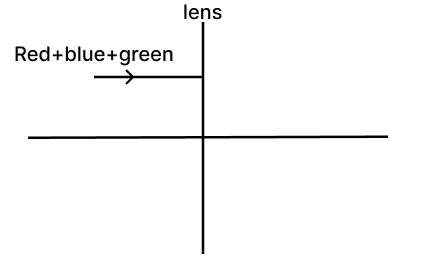
(a) Mixture of red + blue + green is passed through a convex lens as shown in the diagram below. State whether the ray passes through a single point or through different points on the principal axis after refraction.
(b) Name the invisible radiations which are studied using the quartz prism.
(c) State one use of these radiations.
(d) Name one radiation having the wavelength longer than the wavelength of these radiations.