Draw an angle ABC = 60°. Draw the bisector of it. Also draw a line parallel to BC at a distance of 2.5 cm from it.

Let this parallel line meet AB at point P and angle bisectors at point Q. Measure the lengths of BP and PQ. Is BP = PQ ?

Steps:

1. Draw a line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius which cuts BC at point X.

3. With X as centre and the same radius as taken in step 2, draw one more arc which cuts the previous arc at point D.

4. Join BD and produce upto any point A.
   ∠ ABC = 60°.

5. With D as centre, draw an arc of same radius as taken in step 2.

6. With X as centre, draw an arc of same radius as taken in step 2 and cutting the previous arc at point E.

7. Join B and E.
   BE is angle bisector of angle ABC.

8. At any point F in line BC, draw FW perpendicular to BC.

9. With F as centre and radius equal to 2.5 cm, draw an arc which cuts FW at point R.

10. At point R, draw RY perpendicular to FR.

11. Produce RY upto any point Z.

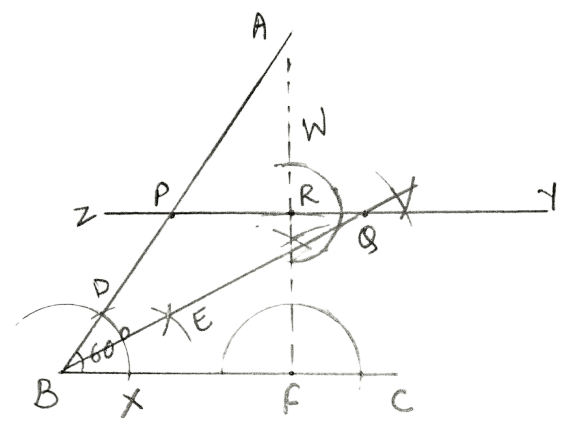
RY is the parallel line to BC at a distance of 2.5 cm from it.

RY meets AB at point P and BE at point Q.

The length of BP = 2.8 cm.

The length of PQ = 2.8 cm.

So, BP = PQ

Hence, the length of BP is equal to that of PQ.