Draw parallelogram ABCD with the following data :

AB = 6 cm, AD = 5 cm and ∠DAB = 45°.

Let AC and DB meet in O and let E be the mid-point of BC. Join OE. Prove that :

(i) OE // AB

(ii) OE = $\dfrac{1}{2}$ AB

In parallelogram,

Opposite sides are equal.

∴ BC = AD = 5.0 cm and CD = AB = 6.0 cm

Steps of construction :

1. Draw a line segment AB = 6.0 cm.

2. Draw AP, such that ∠A = 45°.

3. With A as center and radius equal to 5 cm draw an arc cutting AP at D.

4. With B and D as centers and radii 5.0 cm and 6.0 cm respectively, draw arcs cutting each other at C.

5. Join BC and CD.

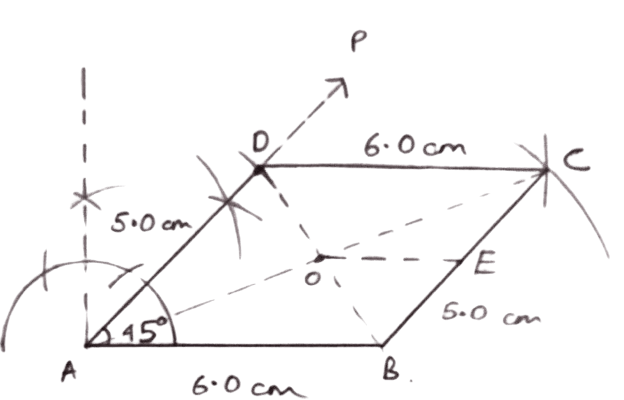
Hence, ABCD is the required parallelogram.

(i) In △ ABC,

O is the mid-point of AC (As diagonals of || gm bisect each other).

E is the mid-point of BC (Given).

By mid-point theorem,

If a line segment joins the mid-point of any two sides of a triangle, then the line segment is said to be parallel to the remaining third side and its measure will be half of the third side.

⇒ OE // AB.

Hence, proved that OE // AB.

(ii) In △ ABC,

O is the mid-point of AC (As diagonals of || gm bisect each other).

E is the mid-point of BC (Given).

By mid-point theorem,

If a line segment joins the mid-point of any two sides of a triangle, then the line segment is said to be parallel to the remaining third side and its measure will be half of the third side.

⇒ OE = $\dfrac{1}{2}AB$.

Hence, proved that OE = $\dfrac{1}{2}AB$.