Mathematics
Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points ?
Answer
Let there be two circles of different radii with centers A and C.
There can be four cases with two circles of different radii :
(i) No point of intersection when circles are away from each other.
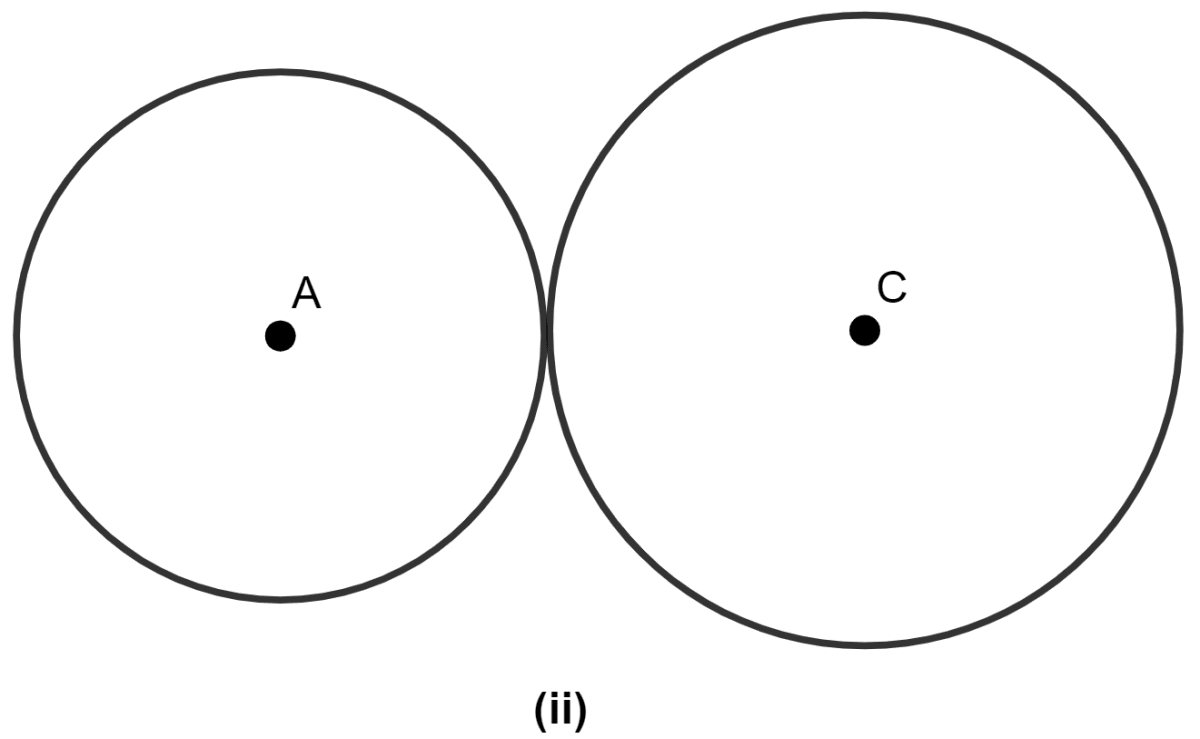
(ii) One point of intersection when circles touch each other.
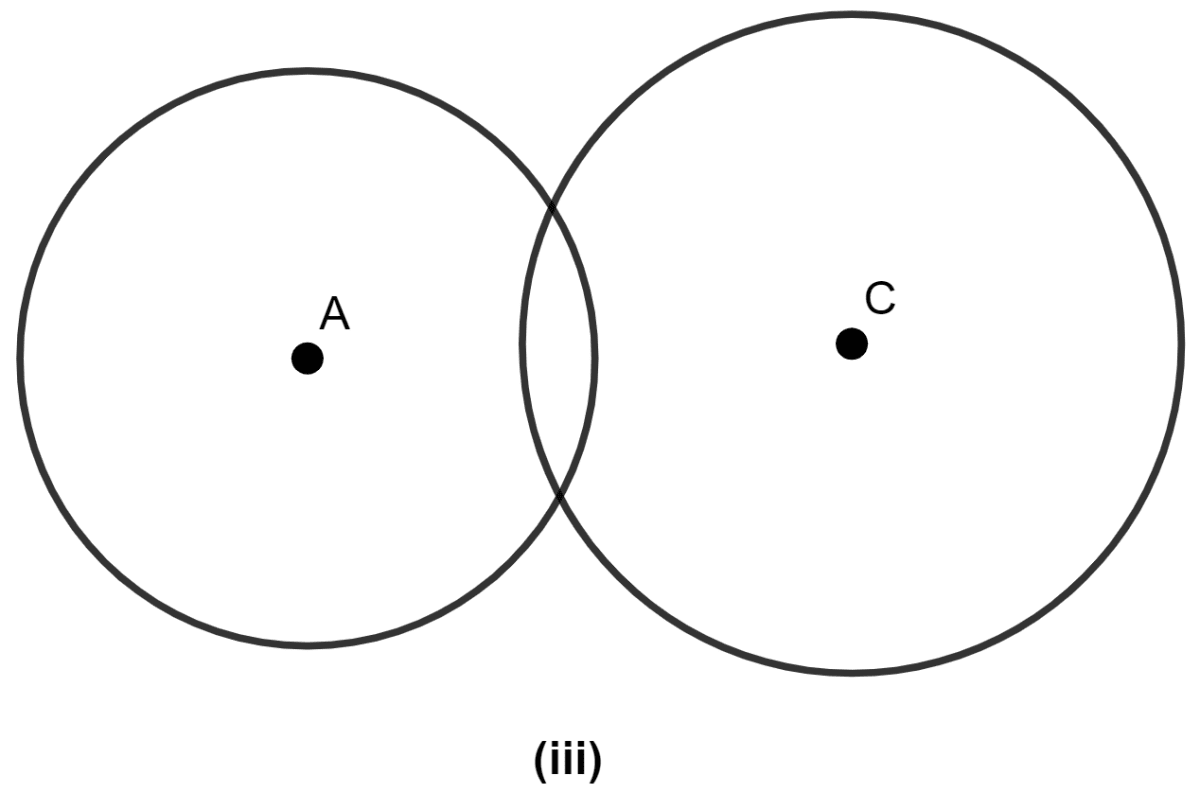
(iii) Two points of intersection when circles intersect each other.
(iv) Infinite, when one circle is completely inside the other and centers are concurrent.
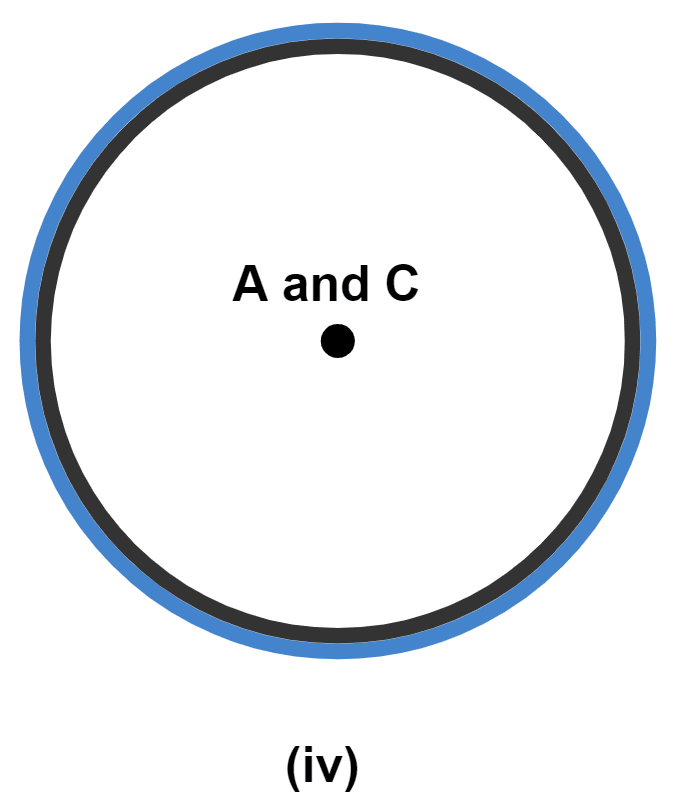
Hence, maximum number of common points are infinite.
Related Questions
The radius of a circle is 13 cm and the length of one of its chords is 24 cm. Find the distance of the chord from the centers.
Prove that equal chords of congruent circles subtend equal angles at their centers.
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
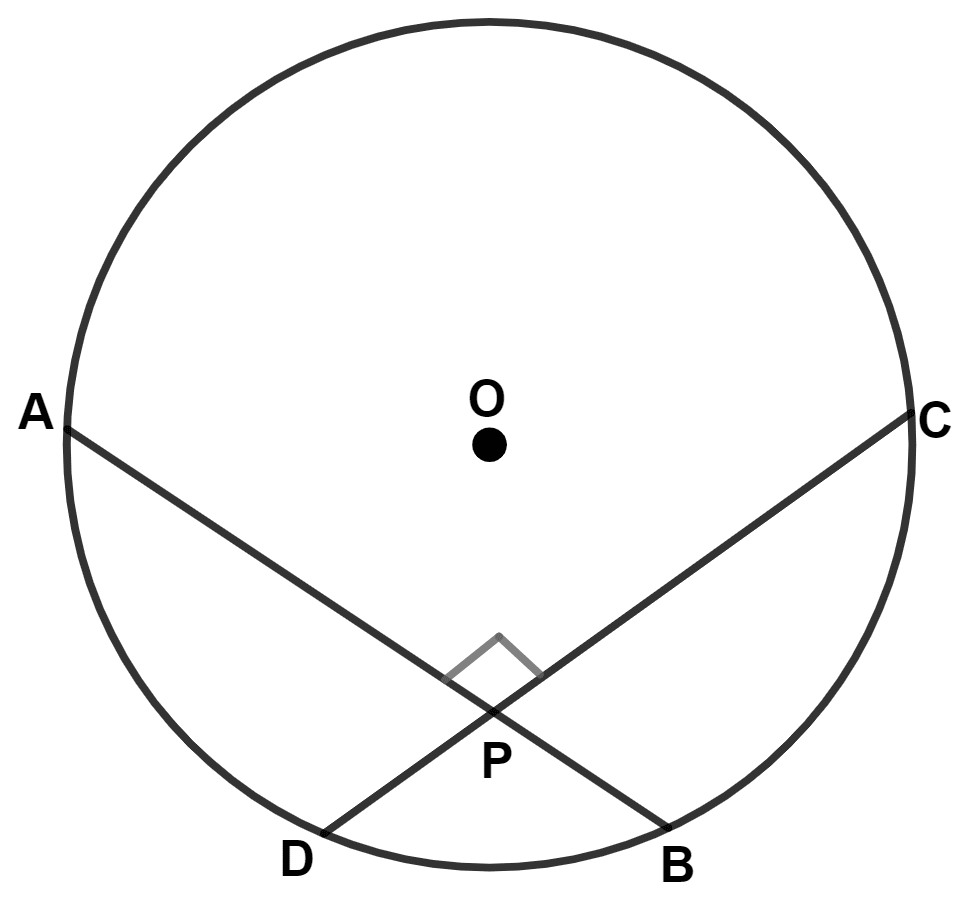
Given two equal chords AB and CD of a circle, with center O, intersecting each other at point P. Prove that :
(i) AP = CP
(ii) BP = DP