Mathematics
Each side of rhombus is 13 cm and one of its diagonals is 10 cm. Find :
(i) the length of its other diagonal
(ii) its area.
Area Trapezium Polygon
21 Likes
Answer
(i) Given :
AB = 13 cm
AC = 10 cm
Then, OA = OC = = 5 cm
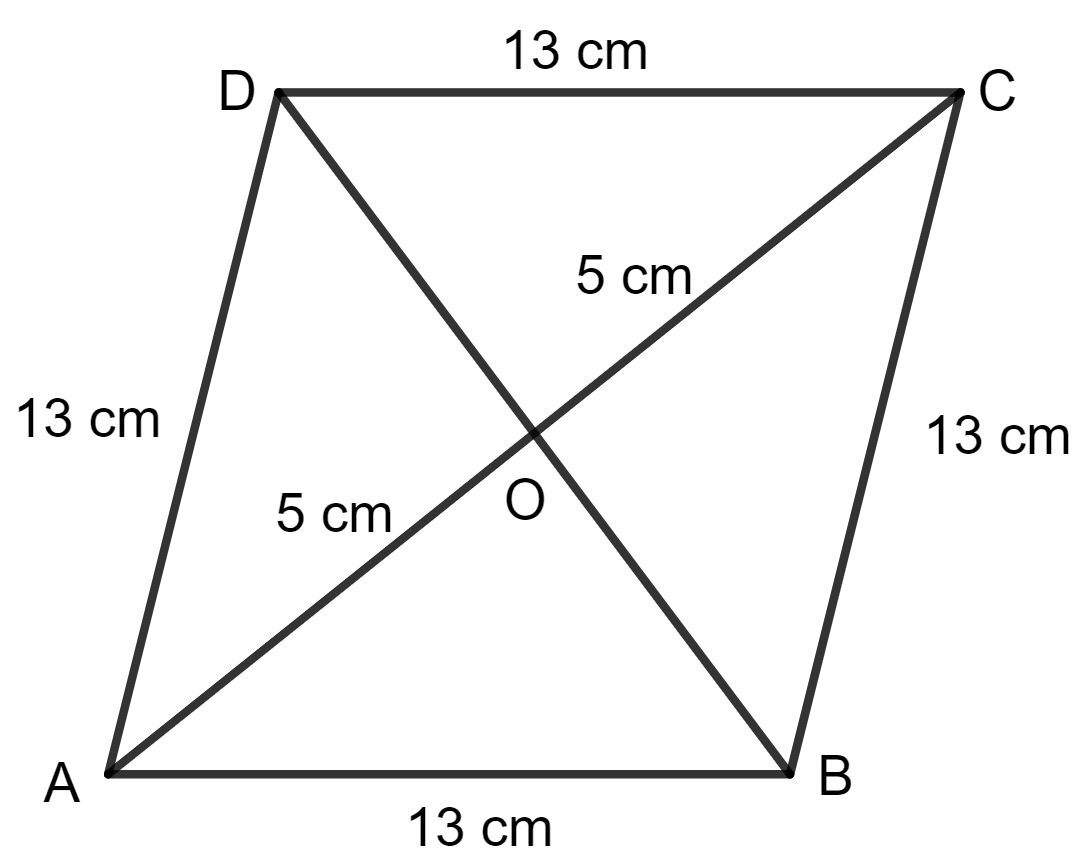
Since the diagonals of a rhombus bisect at 90°.
Applying pythagoras theorem in triangle AOB, we get:
AB2 = OA2 + OB2
⇒ (13)2 = (5)2 + OB2
⇒ 169 = 25 + OB2
⇒ OB2 = 169 - 25
⇒ OB2 = 144
⇒ OB =
⇒ OB = 12
BD = 2 x OB
= 2 x 12 cm
= 24 cm
Hence, the length of other diagonal is 24 cm.
(ii) As we know, the area of rhombus = x product of its diagonal
= x 10 x 24 cm2
= x 240 cm2
= 120 cm2
Hence, the area of the rhombus is 120 cm2.
Answered By
12 Likes
Related Questions
The perimeter of a trapezium is 52 cm. If its non-parallel sides are 10 cm each and its altitude is 8 cm, find the area of the trapezium.
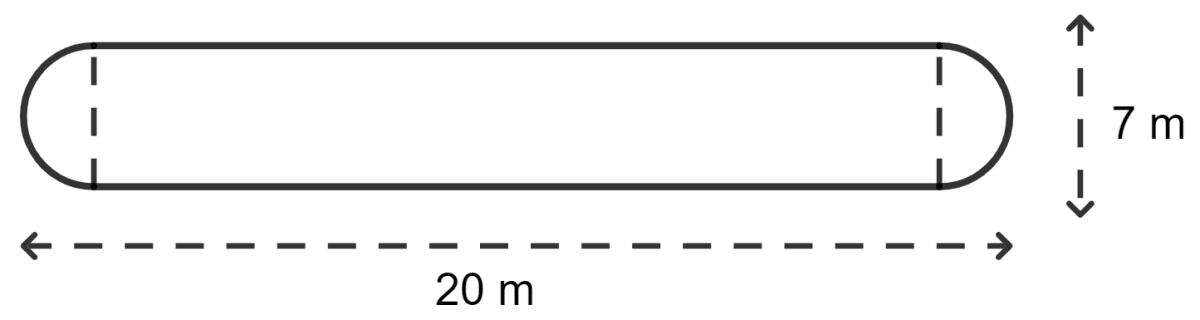
The shape of a garden is rectangular in the middle and semicircular at each end as shown in the figure. Find the area and perimeter of the garden.
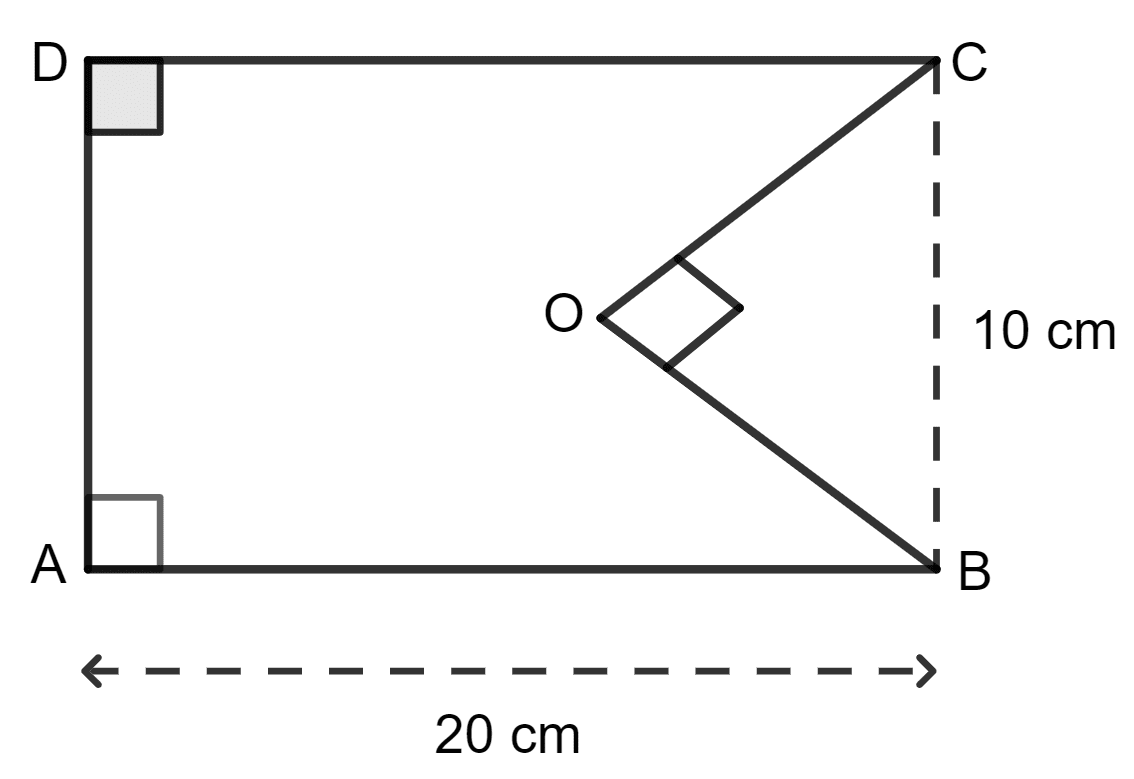
The given figure shows a rectangle ABCD and a right triangle BOC. Find the area of the shaded portion.
Find the area of the circle whose circumference is 264 cm.