Mathematics
An empty tank can be filled by one pipe in 'x' minutes and emptied by another pipe in (x + 5) minutes. Both the pipes, when opened together, can fill the empty tank in 16.8 minutes. Find the value of x.
Quadratic Equations
10 Likes
Answer
Given,
An empty tank can be filled by one pipe in 'x' minutes.
Tank filled by one pipe in a minute =
Tank is emptied by another pipe in (x + 5) minutes.
Tank emptied by another pipe in a minute =
When both pipes are working together, tank filled in 1 minute =
Given,
Both the pipes, when opened together, can fill the empty tank in 16.8 minutes.
So, in one minute, when both the pipes are opened together, tank filled =
Since. no. of minutes cannot be negative.
∴ x = 7.
Hence, x = 7.
Answered By
5 Likes
Related Questions
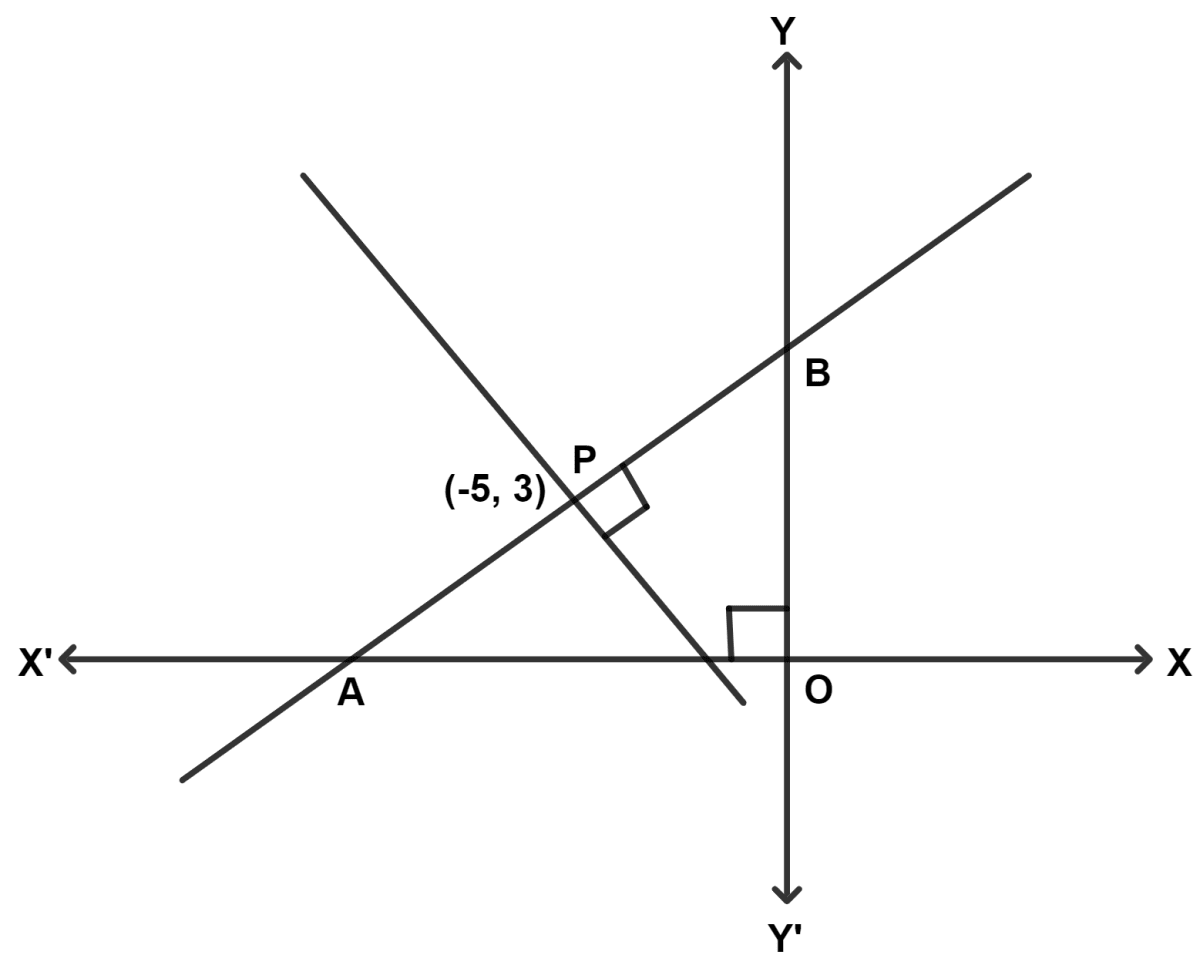
In the given figure, the line segment AB meets x-axis at point A and y-axis at point B.
The point P(-5, 3) on AB divides it in the ratio 3 : 2. Find :
(i) co-ordinates of point A
(ii) co-ordinates of point B
(iii) equation of line through point P and perpendicular to AB.
(iv) the point of intersection of the line (obtained in part (iii) above) and x-axis.
If , find the value of ax + by + cz.
Use ruler and compass only to construct a triangle ABP such that AB = 8 cm, BP = 5 cm and angle ABP = 30°.
(i) Complete the rhombus ABCD such that P is equidistant from AB and BC.
(ii) Locate a point Q on line BP such that Q is equidistant from A and B.
Using remainder and factor theorem, factorize completely, the given polynomial :
2x3 + x2 - 13x + 6