Mathematics
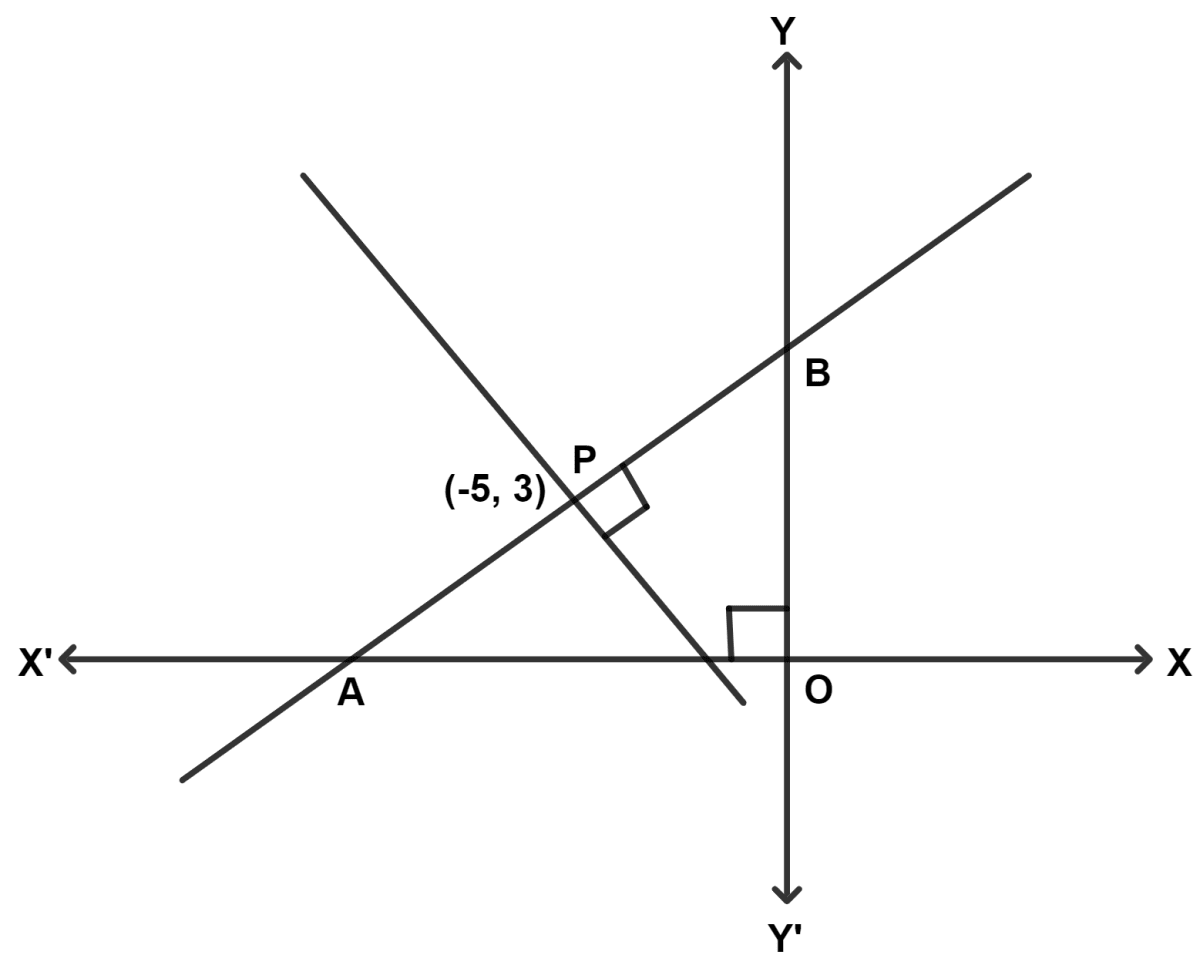
In the given figure, the line segment AB meets x-axis at point A and y-axis at point B.
The point P(-5, 3) on AB divides it in the ratio 3 : 2. Find :
(i) co-ordinates of point A
(ii) co-ordinates of point B
(iii) equation of line through point P and perpendicular to AB.
(iv) the point of intersection of the line (obtained in part (iii) above) and x-axis.
Straight Line Eq
17 Likes
Answer
Let co-ordinates of A be (a, 0) and B be (0, b).
Given, P(-5, 3) on AB divides it in the ratio 3 : 2.
By section formula,
(x, y) =
Substituting values we get :
A = (a, 0) =
B = (0, b) = (0, 5).
(i) Hence, co-ordinates of A = .
(ii) Hence, co-ordinates of B = (0, 5).
(iii) By formula,
Slope =
Slope of AB
= .
We know that,
Product of slope of perpendicular lines = -1.
Let slope of line perpendicular to AB be a.
⇒ = -1
⇒ a = .
By point-slope form,
Equation of line : y - y1 = m(x - x1)
Substituting values we get :
⇒ y - 3 = [x - (-5)]
⇒ 2(y - 3) = -5(x + 5)
⇒ 2y - 6 = -5x - 25
⇒ 2y + 5x - 6 + 25 = 0
⇒ 2y + 5x + 19 = 0.
Hence, equation of line through point P and perpendicular to AB is 2y + 5x + 19 = 0.
(iv) Any point on x-axis is given by (x1, 0).
Substituting values in equation 2y + 5x + 19 = 0, we get :
⇒ 2(0) + 5x1 + 19 = 0
⇒ 5x1 + 19 = 0
⇒ 5x1 = -19
⇒ x1 =
⇒ (x1, 0) = .
Hence, point of intersection = .
Answered By
10 Likes
Related Questions
Find the smallest value of x for the inequation x - 3(2 + x) < 2(3x - 1) when :
(i) x ∈ W (whole numbers)
(ii) x ∈ N (natural numbers)
(iii) x ∈ I (integers)
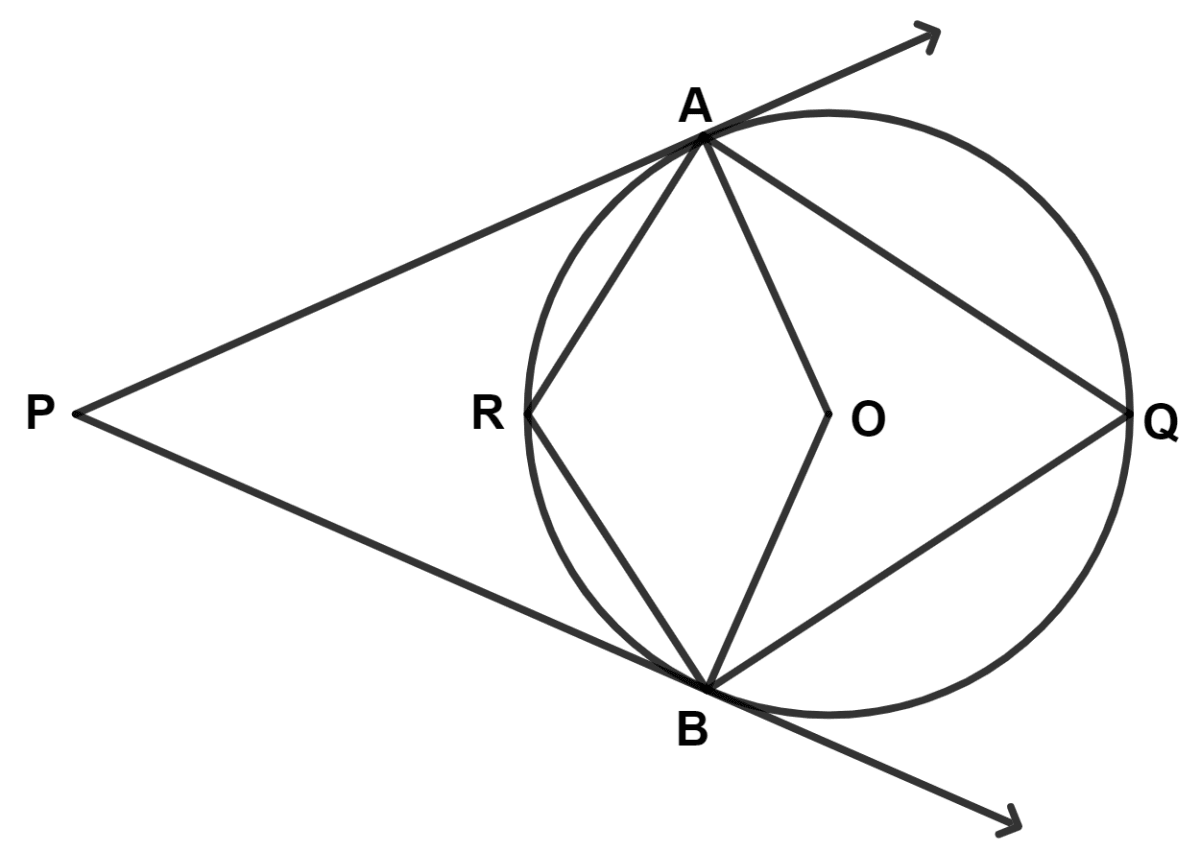
In the given figure, PA and PB are tangents at the points A and B respectively of a circle with center O. Q and R are points on the circle, if ∠APB = 70°, find :
(i) reflex angle AOB
(ii) ∠AQB
(iii) ∠ARB
If , find the value of ax + by + cz.
An empty tank can be filled by one pipe in 'x' minutes and emptied by another pipe in (x + 5) minutes. Both the pipes, when opened together, can fill the empty tank in 16.8 minutes. Find the value of x.