Mathematics
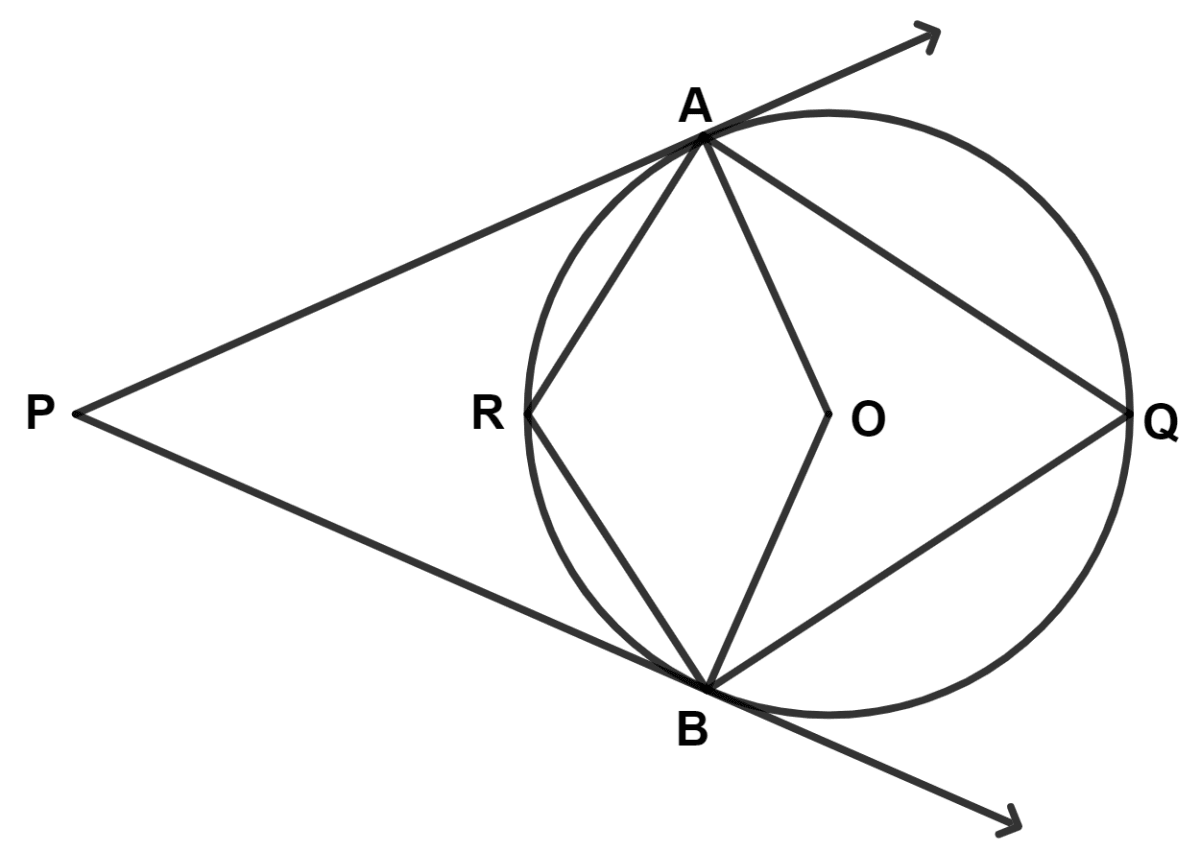
In the given figure, PA and PB are tangents at the points A and B respectively of a circle with center O. Q and R are points on the circle, if ∠APB = 70°, find :
(i) reflex angle AOB
(ii) ∠AQB
(iii) ∠ARB
Circles
10 Likes
Answer
(i) AP and BP are tangents to the circle and OA and OB are radius of the circle.
∴ OA ⊥ AP and OB ⊥ BP.
∴ ∠OAP = ∠OBP = 90°
Sum of angles of a quadrilateral = 360°.
Hence, in quadrilateral OAPB,
⇒ ∠APB + ∠OAP + ∠OBP + ∠AOB = 360°
⇒ 70° + 90° + 90° + ∠AOB = 360°
⇒ 250° + ∠AOB = 360°
⇒ ∠AOB = 360° - 250°
⇒ ∠AOB = 110°.
Reflex angle AOB = 360° - ∠AOB = 360° - 110° = 250°.
Hence, the value of reflex ∠AOB = 250°.
(ii) Arc AB subtends ∠AOB at centre and ∠AQB at remaining part of circle.
∴ ∠AOB = 2∠AQB (As angle at centre is double the angle subtended at remaining part of circle.)
⇒ 110° = 2∠AQB
⇒ ∠AQB = = 55°.
Hence, the value of ∠AQB = 55°.
(iii) Reflex ∠AOB = 250°.
Arc AB subtends Reflex ∠AOB at centre and ∠ARB at remaining part of circle.
∴ Reflex ∠AOB = 2∠ARB (As angle at centre is double the angle subtended at remaining part of circle.)
⇒ 2∠ARB = 250°
⇒ ∠ARB =
⇒ ∠ARB = 125°.
Hence, the value of ∠ARB = 125°.
Answered By
4 Likes
Related Questions
From the top of a 80 m high tower, the angles of depression of two men, on either sides of the tower, are found to be 32° and 58°. Find the distance between the two men correct to the nearest whole numbers.
Find the smallest value of x for the inequation x - 3(2 + x) < 2(3x - 1) when :
(i) x ∈ W (whole numbers)
(ii) x ∈ N (natural numbers)
(iii) x ∈ I (integers)
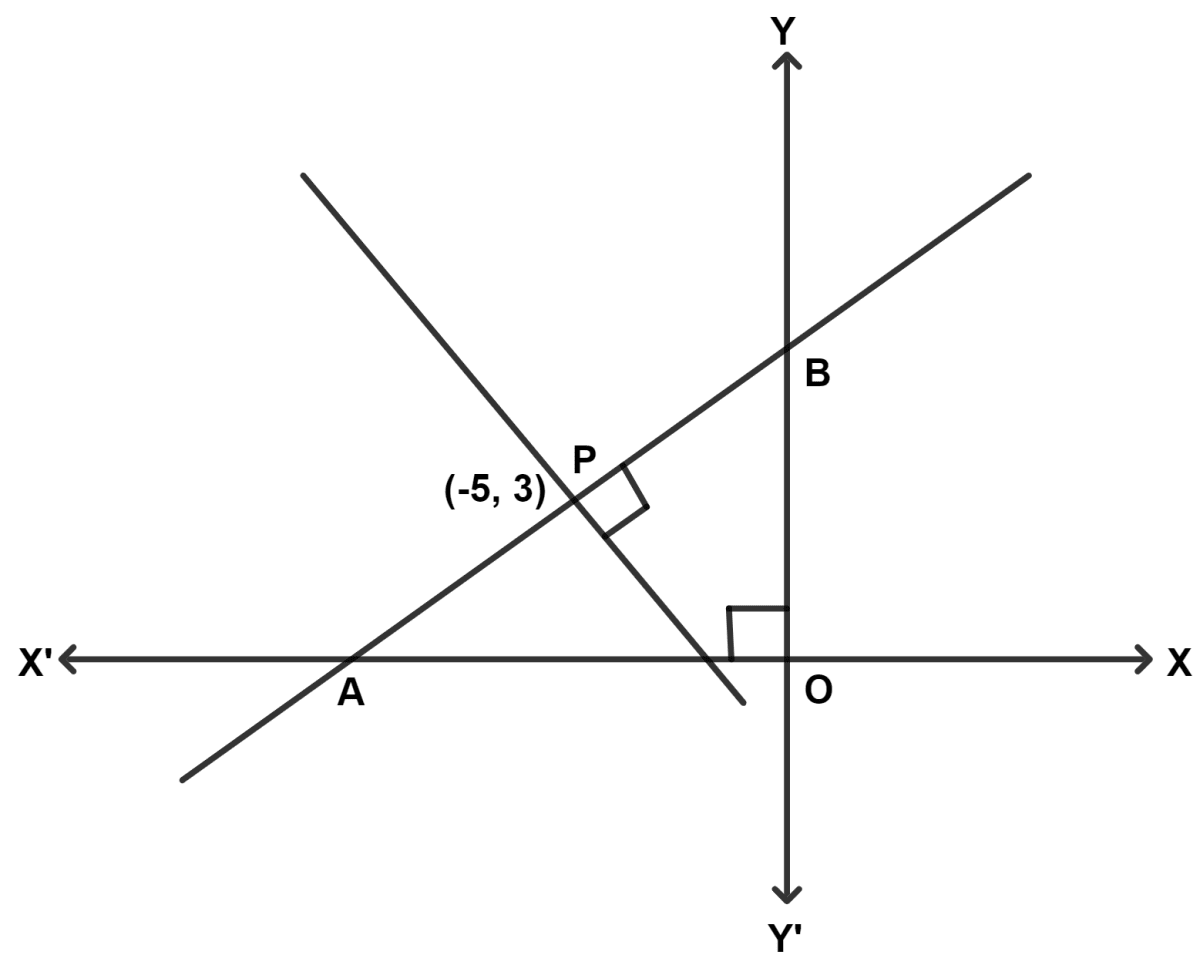
In the given figure, the line segment AB meets x-axis at point A and y-axis at point B.
The point P(-5, 3) on AB divides it in the ratio 3 : 2. Find :
(i) co-ordinates of point A
(ii) co-ordinates of point B
(iii) equation of line through point P and perpendicular to AB.
(iv) the point of intersection of the line (obtained in part (iii) above) and x-axis.
If , find the value of ax + by + cz.