Mathematics
Find the distance of point (8, -4) from y-axis.
Graphical Solution
6 Likes
Answer
Plot the point (8, -4) on the graph paper.
Draw a perpendicular line from the point (8, -4) to the y-axis.
From graph it is clear that the distance between the point (8,−4) and the y-axis is 8 units.
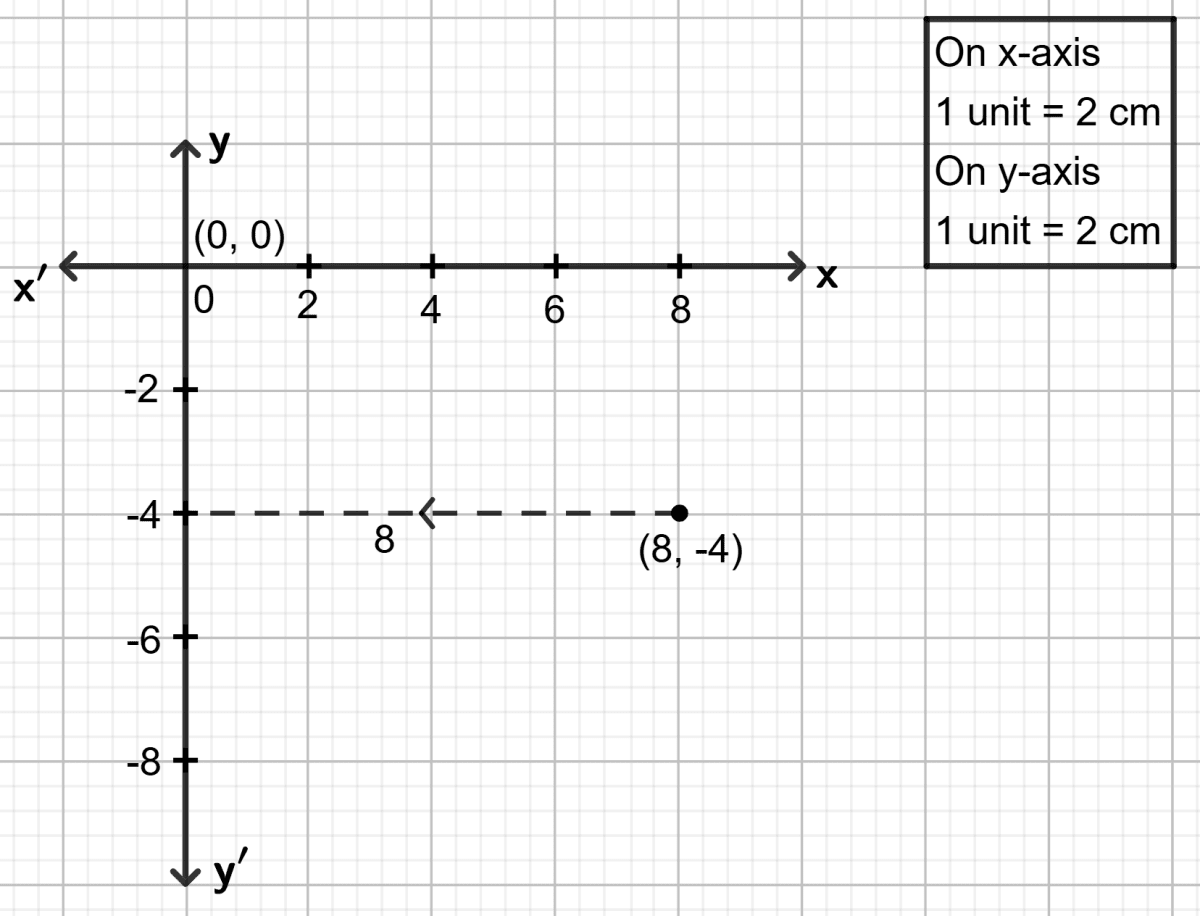
Hence, the distance of point (8, -4) from y-axis is 8 units.
Answered By
4 Likes
Related Questions
Assertion (A): y + 5 = 0 is the equation of line parallel to x-axis and at the distance of 5 unit in the negative direction from it.
Reason (R): For all the points on the y = a (a constant), the value of abscissa is a.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Assertion (A): For the line 3x + 4y = 7, the abscissa is .
Reason (R): 3x + 4y = 7
⇒ 3x = 7
and x = .
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Three vertices of parallelogram ABCD are A(-5, -1), B(3, -1) and C(1, -6). Use graphical method to find the co-ordinates of fourth vertex D.
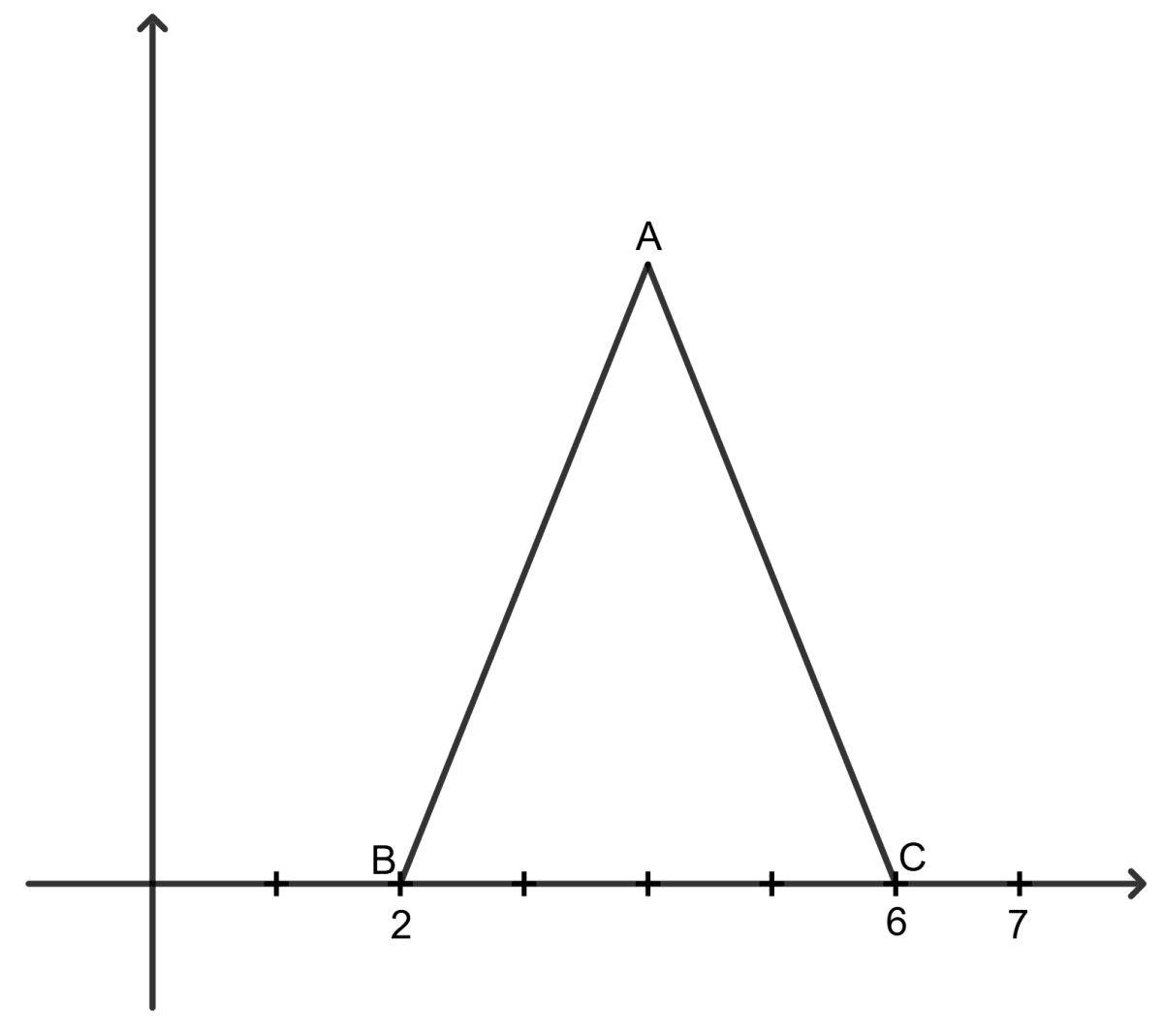
In the given figure, ABC is an equilateral triangle. Find the co-ordinates of A.