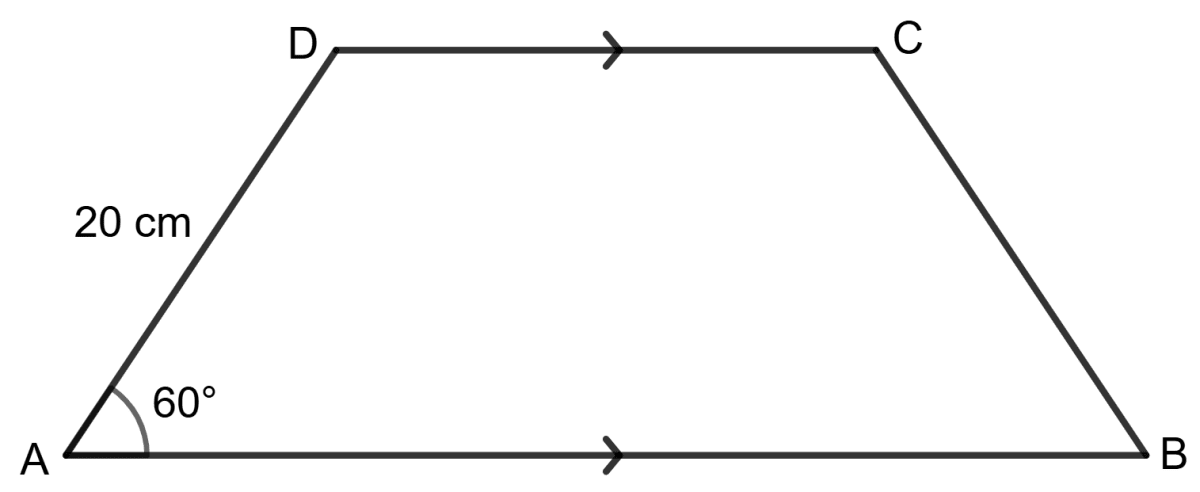
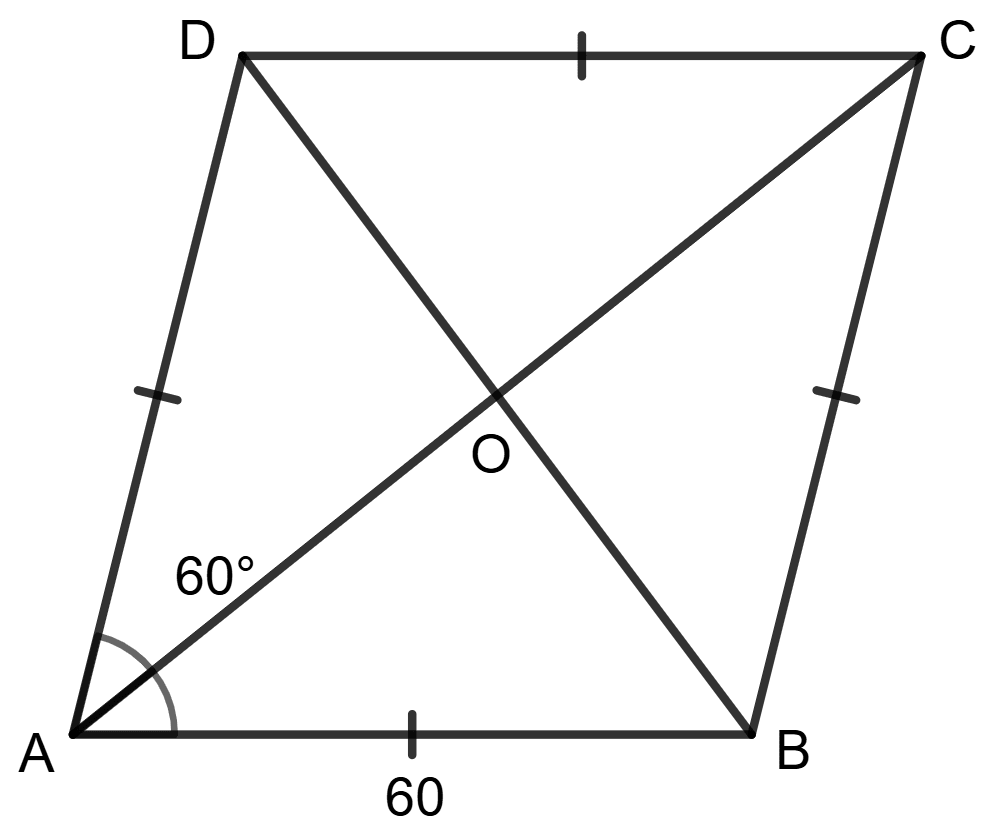
Find lengths of diagonals AC and BD.

Given AB = 60 cm and ∠BAD = 60°.

ABCD is a rhombus as AB = BC = CD = DA and ∠ BAD = 60°.

Now in Δ ABD,

AB = AD (Sides of rhombus)

⇒ ∠ ABD = ∠ ADB (Angles opposite to equal side of Δ)

Let ∠ ABD = x.

According to the angle sum property,

∠ ABD + ∠ ADB + ∠ BAD = 180°

⇒ x + x + 60° = 180°

⇒ 2x + 60° = 180°

⇒ 2x = 180° - 60°

⇒ 2x = 120°

⇒ x = $\dfrac{120°}{2}$

⇒ x = 60°

ABCD is a rhombus. So, diagonals AC and BD bisect each other at 90°.

AO = OC and BO = OD

In Δ AOD,

$\text{cos 60°} = \dfrac{Base}{Hypotenuse}\\[1em] ⇒ \dfrac{1}{2} = \dfrac{OD}{60}\\[1em] ⇒ OD = \dfrac{60}{2} = 30$

And,

$\text{sin 60°} = \dfrac{Perpendicular}{Hypotenuse}\\[1em] ⇒ \dfrac{\sqrt3}{2} = \dfrac{AO}{60}\\[1em] ⇒ AO = \dfrac{60\sqrt3}{2} = 51.96$

AC = 2 x AO = 2 x 51.96 = 103.92 cm

BD = 2 x BO = 2 x 30 = 60 cm

Hence, AC = 103.92 cm and BD = 60 cm.