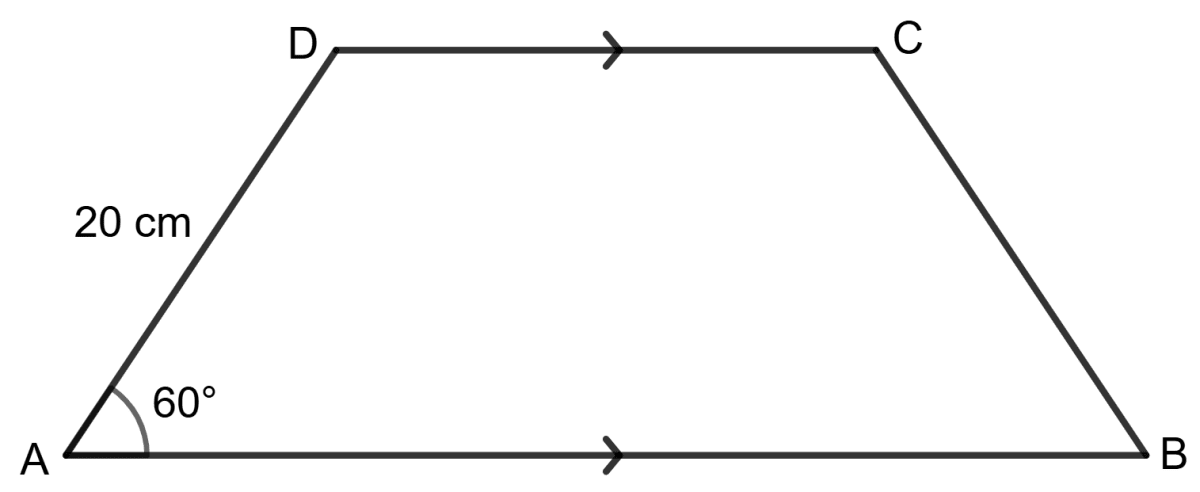
In trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠A = 60°.

Find :

(i) length of AB

(ii) distance between AB and DC.

(i) Draw two perpendicular lines, DP and CM, from points D and C to AB, respectively. Since AB is parallel to CD, PMCD will form a rectangle.

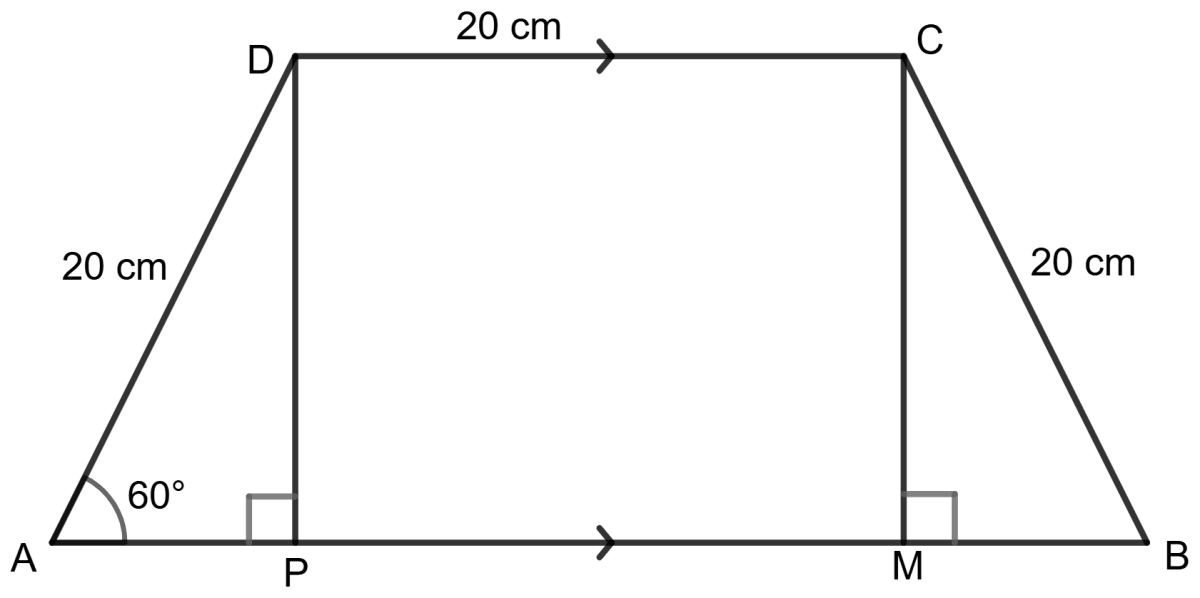
In Δ APD,

cos 60° = $\dfrac{Base}{Hypotenuse}$

⇒ $\dfrac{1}{2} = \dfrac{AP}{AD}$

⇒ $\dfrac{1}{2} = \dfrac{AP}{20}$

⇒ AP = 10

Now, Δ APD and Δ BMC,

DP = CM (Height of same quadrilateral)

AD = CB (Both are 20 cm)

∠ DPA = ∠ CMB

So, Δ APD ≅ Δ BMC (∵ RHS congruency)

And, by using corresponding sides of congruent triangle,

AP = MB = 10 cm

PM = DC = 20 cm

AB = AP + PM + MB

= 10 + 20 + 10 cm

= 40 cm

Hence, AB = 40 cm.

(ii) In Δ APD,

sin 60° = $\dfrac{Perpendicular}{Hypotenuse}$

⇒ $\dfrac{\sqrt3}{2} = \dfrac{PD}{AD}$

⇒ $\dfrac{\sqrt3}{2} = \dfrac{PD}{20}$

⇒ PD = 10 $\sqrt3$ = 17.32 cm

Hence, PD = 17.32 cm.