Mathematics
Find the area of a quadrilateral one of whose diagonals is 30 cm long and the perpendiculars from the other two vertices are 19 cm and 11 cm respectively.
Mensuration
38 Likes
Answer
The quadrilateral is shown in the figure below:
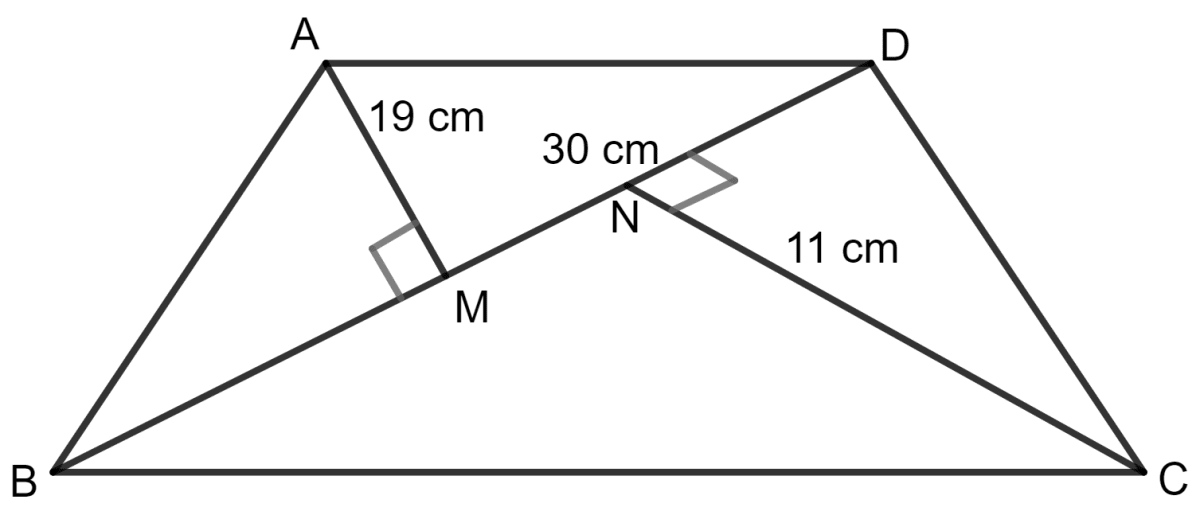
Area of triangle = x base x height
For Δ ABD,
Area = x BD x AM
= x 30 x 19 cm2
= 15 x 19 cm2
= 285 cm2
For Δ CBD,
Area = x BD x CN
= x 30 x 11 cm2
= 15 x 11 cm2
= 165 cm2
Area of quadrilateral ABCD = Area of Δ ABD + Area of Δ CBD
= 285 + 165 cm2
= 450 cm2
Hence, the area of quadrilateral is 450 cm2.
Answered By
21 Likes
Related Questions
The perimeter of a square is 72 cm, its area is :
324 cm2
356 cm2
Area of a rhombus is 360 cm2. If one diagonal of it is 20 cm; the other diagonal is :
24 cm
18 cm
40 cm
36 cm
The diagonals of a quadrilateral are 16 cm and 13 cm. If they intersect each other at right angles; find the area of the quadrilateral.
Calculate the area of quadrilateral ABCD, in which ∠ABD = 90°, triangle BCD is an equilateral triangle of side 24 cm and AD = 26 cm.