Mathematics
In the following figure, AB = AC, EC = ED, ∠ABF = 45° and ∠ABC = 70°.
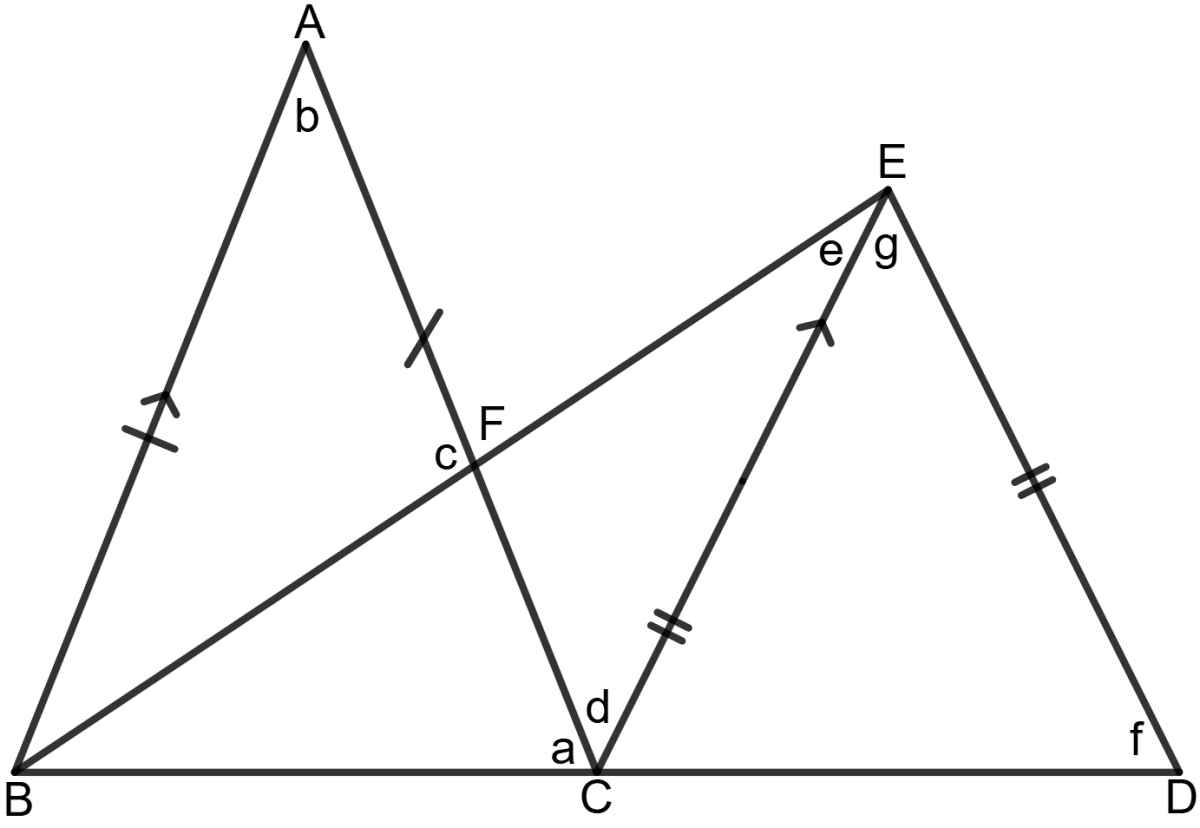
Find the angles represented by letters a, b, c, d, e, f and g.
Triangles
4 Likes
Answer
Given: AB = AC (Isosceles triangle)
EC = ED (Isosceles triangle)
∠ABF = 45°
∠ABC = 70°
Since AB = AC, the angles opposite to equal sides are also equal:
⇒ ∠ABC = ∠ACB
⇒ a = 70°
Using the angle sum property of Δ ABC:
⇒ ∠ABC + ∠ACB + ∠BAC = 180°
⇒ 70° + 70° + b = 180°
⇒ 140° + b = 180°
⇒ b = 180° - 140°
⇒ b = 40°
Using the angle sum property in Δ ABF:
⇒ ∠ABF + ∠AFB + ∠BAF = 180°
⇒ 45° + c + 40° = 180°
⇒ 85° + c = 180°
⇒ c = 180° - 85°
⇒ c = 95°
Since ∠AFB and ∠EFC are Vertically opposite angles,
⇒ ∠EFC = c = 95°
Since ∠BAC = b and ∠BAC is alternate to ∠ACE,
⇒ d = b = 40°
Using the angle sum property in Δ EFC,
⇒ ∠EFC + ∠ECF + ∠FEC = 180°
⇒ 95° + 40° + e = 180°
⇒ 135° + e = 180°
⇒ e = 180° - 135° = 45°
Since ∠ACE and ∠CED are alternate angles,
⇒ g = d = 40°
Since EC = ED, the angles opposite to equal sides are also equal.
⇒ ∠ECD = ∠EDC = f
Using the angle sum property in Δ ECD,
⇒ ∠ECD + ∠EDC + ∠DEC = 180°
⇒ f + f + 40° = 180°
⇒ 2f + 40° = 180°
⇒ 2f = 180° - 40°
⇒ 2f = 140°
⇒ f = = 70°
Hence, a = 70°, b = 40°, c = 95°, d = 40°, e = 45°, f = 70° and g = 40°.
Answered By
2 Likes
Related Questions
State, true or false, for each of the following statements.
(i) If three angles of two triangles are equal, the triangles are congruent.
(ii) If two sides of a right triangle, containing right angle, are equal to corresponding sides of another right triangle, the triangle are congruent.
(iii) If two triangles are congruent, then the corresponding angles are equal.
(iv) If two angles and a side of one triangle are equal to two angles and a side of another triangle, the triangles are congruent.
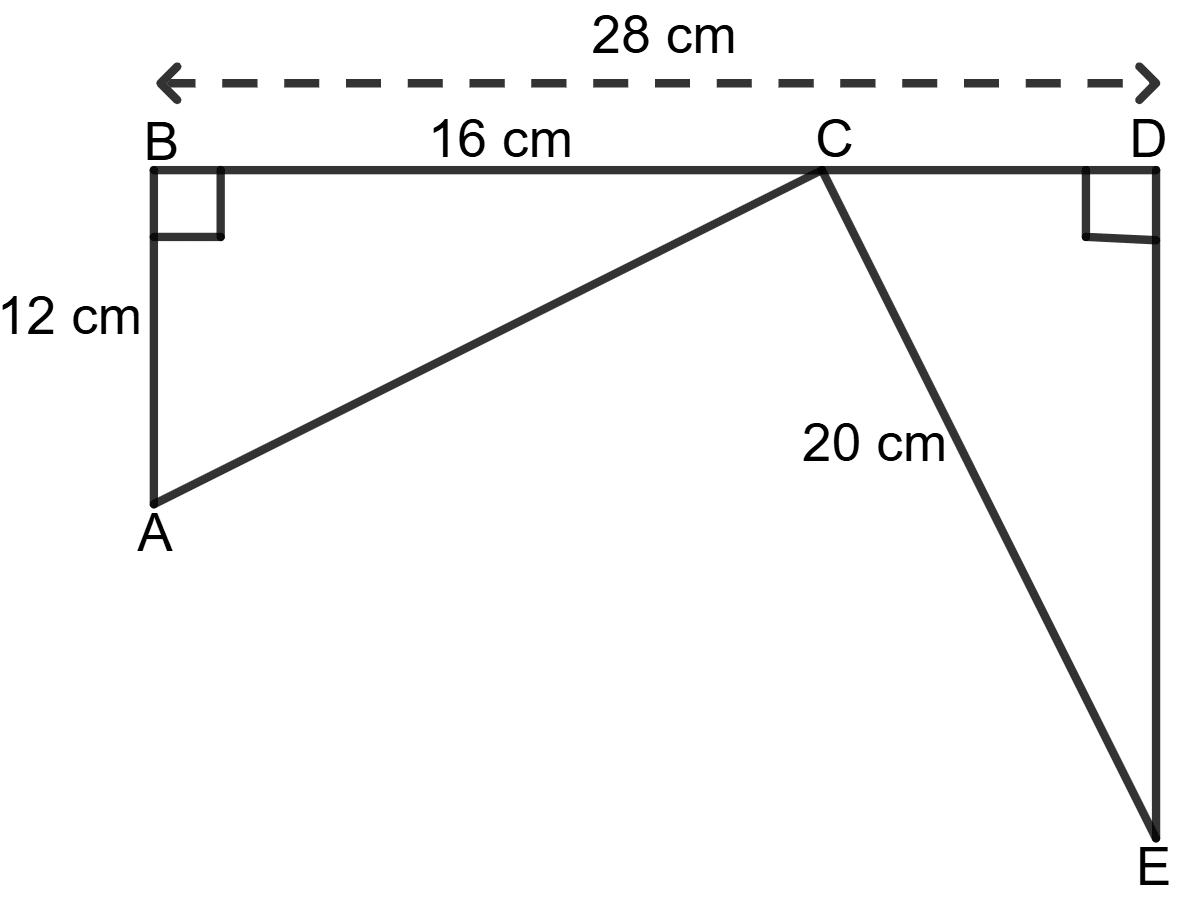
Show that the two triangles given in the following figure are congruent.
In the figure, given below, AB is parallel to CD and CA = CE.
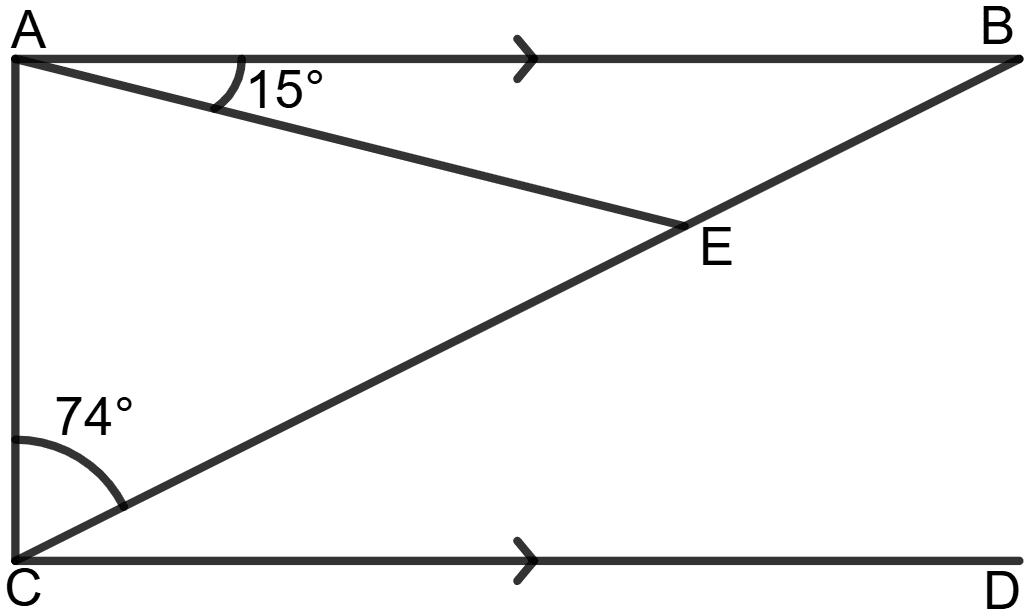
If angle ACE = 74° and angle EAB = 15°, find the angles AEB and BCD.
In the given figure, AD = DB = DE, ∠EAC = ∠FAC and ∠F = 90°
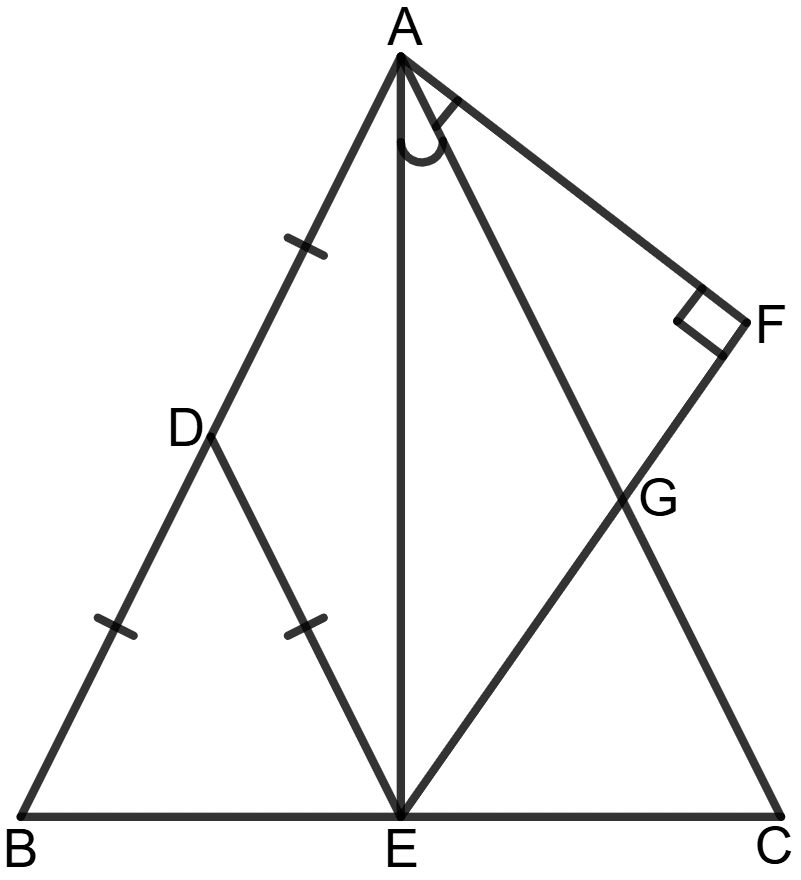
Prove that :
(i) ∠AEB = 90°
(ii) △ CEG is isosceles
(iii) ∠CEG = ∠EAF.