Mathematics
In the figure, given below, AB is parallel to CD and CA = CE.
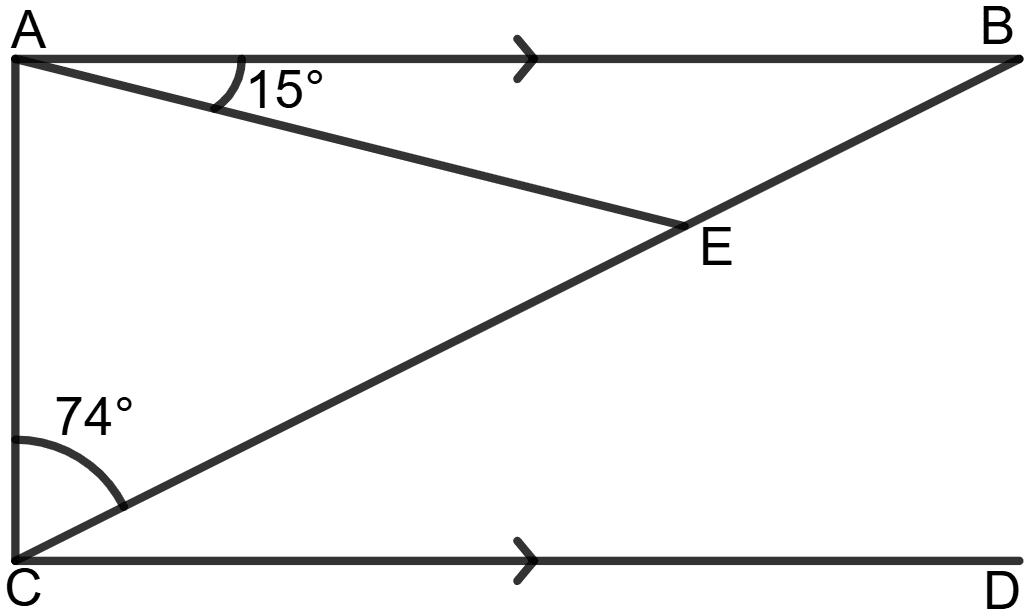
If angle ACE = 74° and angle EAB = 15°, find the angles AEB and BCD.
Triangles
2 Likes
Answer
Given: AB // CD, CA = CE
∠ACE = 74°, ∠EAB = 15°
Since CA = CE, the angles opposite to equal sides are also equal:
∠CAE = ∠CEA = a
Using the angle sum property in Δ ACE,
⇒ ∠ACE + ∠AEC + ∠EAC = 180°
⇒ 74° + a + a = 180°
⇒ 74° + 2a = 180°
⇒ 2a = 180° - 74°
⇒ 2a = 106°
⇒ a =
⇒ a = 53°
So, ∠CAE = ∠CEA = 53°.
Since ∠CEA and ∠AEB form a linear pair,
∠CEA + ∠AEB = 180°
⇒ 53° + ∠AEB = 180°
⇒ ∠AEB = 180° - 53°
⇒ ∠AEB = 127°
In Δ AEB, using the angle sum property:
⇒ ∠AEB + ∠ABE + ∠EAB = 180°
⇒ 127° + ∠ABE + 15° = 180°
⇒ 142° + ∠ABE = 180°
⇒ ∠ABE = 180° - 142°
⇒ ∠ABE = 38°
Since AB || CD, ∠BCD = ∠ABE (corresponding angles property):
∠BCD = 38°
Hence, ∠AEB = 127° and ∠BCD = 38°.
Answered By
2 Likes
Related Questions
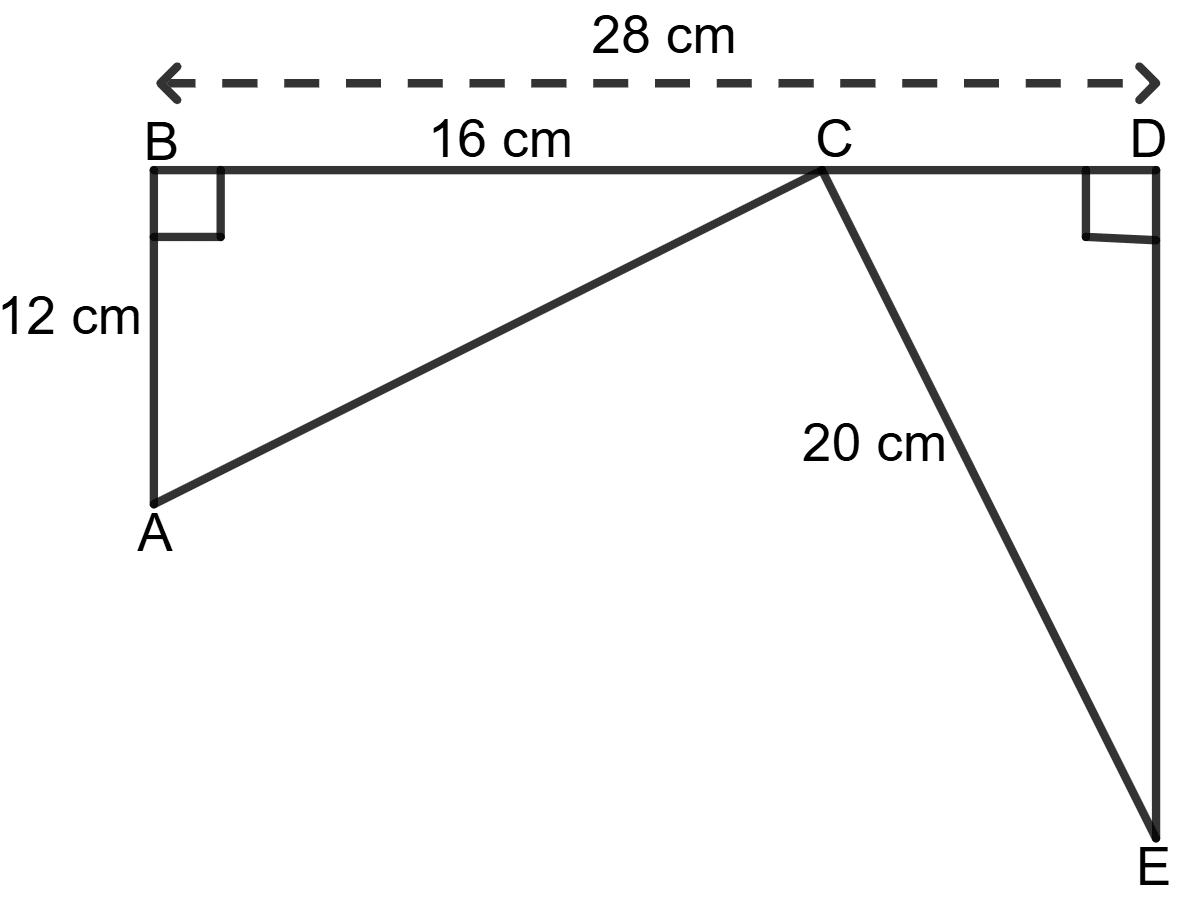
Show that the two triangles given in the following figure are congruent.
In the following figure, AB = AC, EC = ED, ∠ABF = 45° and ∠ABC = 70°.
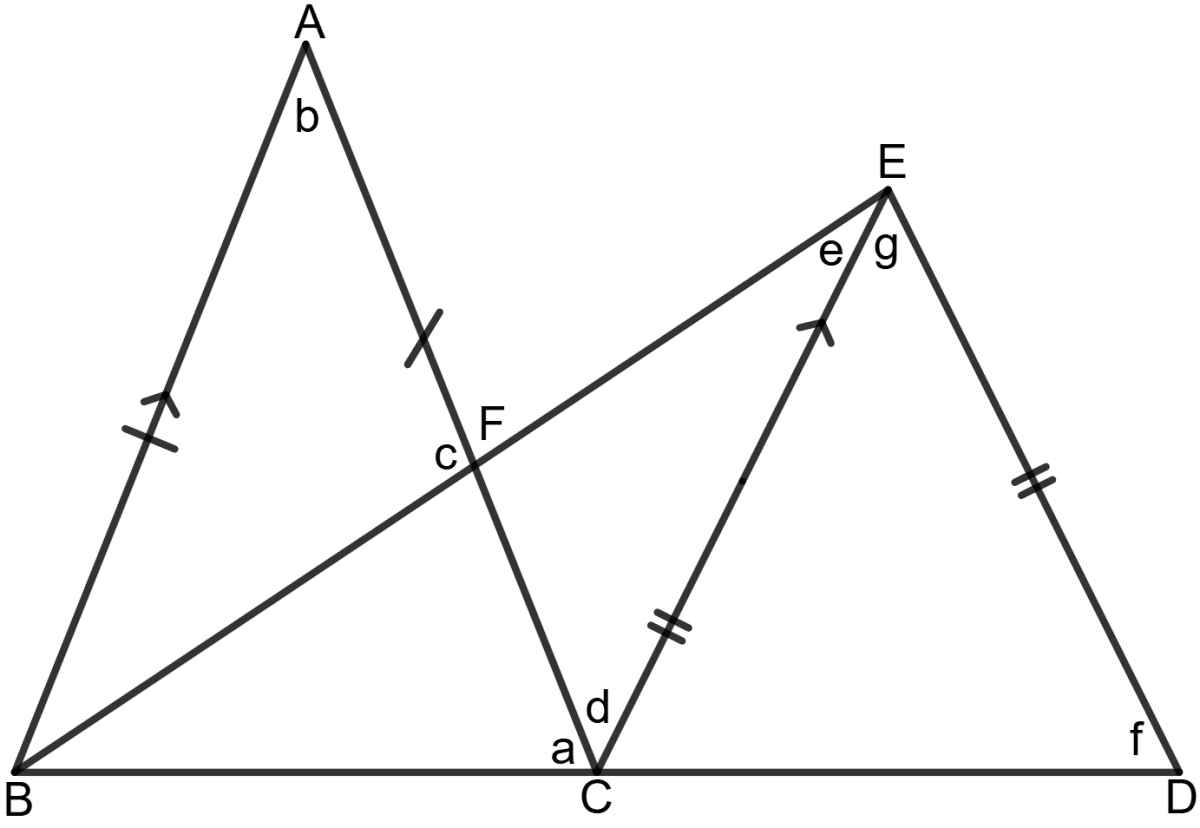
Find the angles represented by letters a, b, c, d, e, f and g.
In the given figure, AD = DB = DE, ∠EAC = ∠FAC and ∠F = 90°
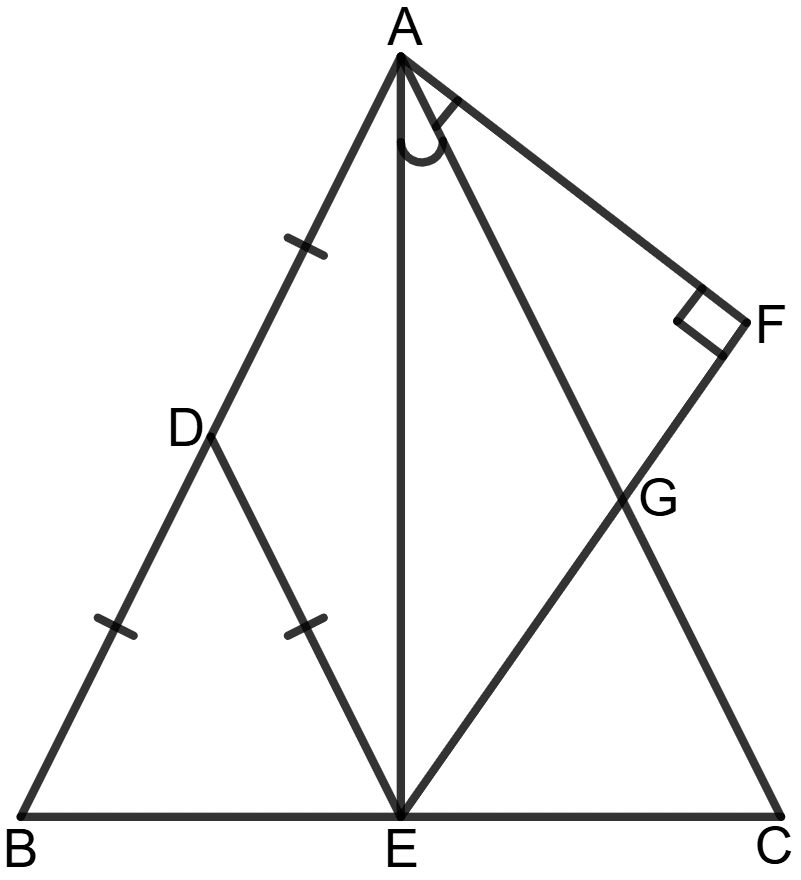
Prove that :
(i) ∠AEB = 90°
(ii) △ CEG is isosceles
(iii) ∠CEG = ∠EAF.
(i) In an isosceles triangle the angles are in the ratio 7 : 4 : 7. Find each base angle of the triangle.
(ii) Find the angles of an isosceles triangle, if the ratio of the base angle to the vertical angle 2 : 5.