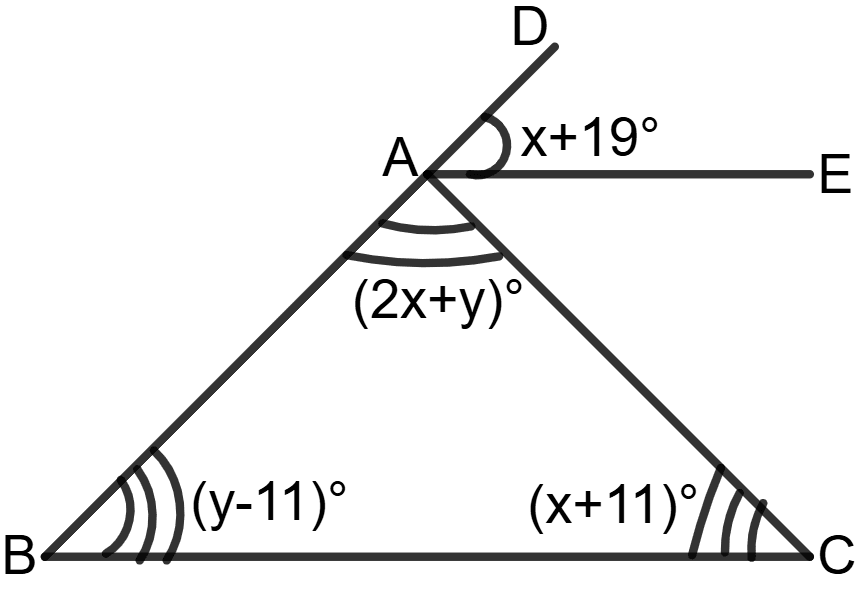Mathematics
(i) In an isosceles triangle the angles are in the ratio 7 : 4 : 7. Find each base angle of the triangle.
(ii) Find the angles of an isosceles triangle, if the ratio of the base angle to the vertical angle 2 : 5.
Triangles
2 Likes
Answer
(i) Given: The angles of the isosceles triangle are in the ratio 7 : 4 : 7.
Let the three angles be 7a, 4a, and 7a.
Using the angle sum property of a triangle:
⇒ 7a + 4a + 7a = 180°
⇒ 18a = 180°
⇒ a =
⇒ a = 10°
Now, the two base angles are:
7a = 7 x 10° = 70°
Hence, the base angles are 70° and 70°.
(ii) Given: The ratio of the base angle to the vertical angle is 2 : 5.
Let each base angle be 2a and the vertical angle be 5a.
Using the angle sum property of a triangle:
⇒ 2a + 5a + 2a = 180°
⇒ 9a = 180°
⇒ a =
⇒ a = 20°
Now, the angles of the triangle are:
2a = 2 x 20° = 40° and 5a = 5 x 20° = 100°
Hence, the angles of isosceles triangle are 40°, 40° and 100°.
Answered By
1 Like
Related Questions
In the figure, given below, AB is parallel to CD and CA = CE.
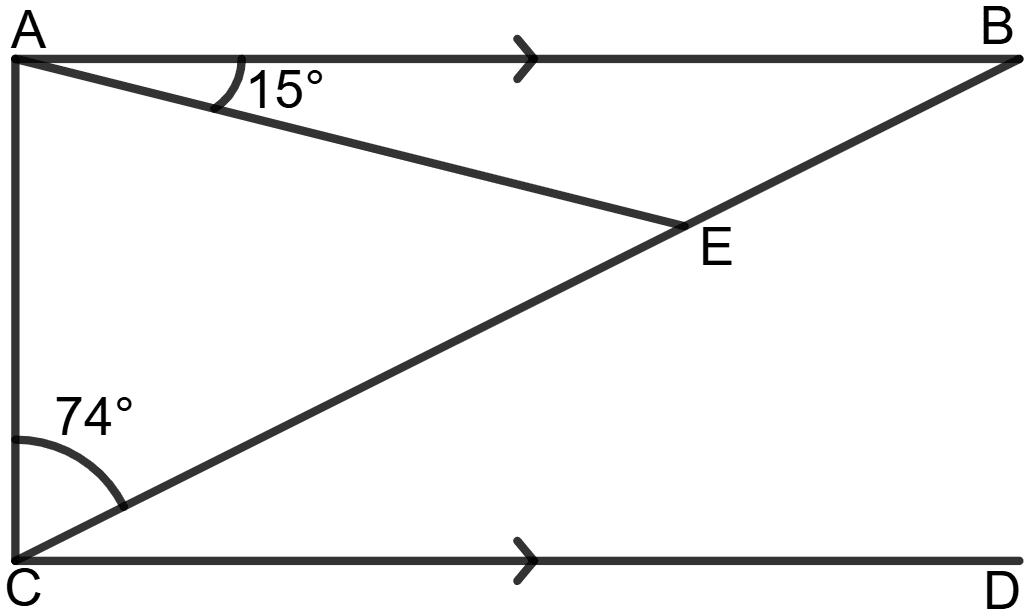
If angle ACE = 74° and angle EAB = 15°, find the angles AEB and BCD.
In the given figure, AD = DB = DE, ∠EAC = ∠FAC and ∠F = 90°
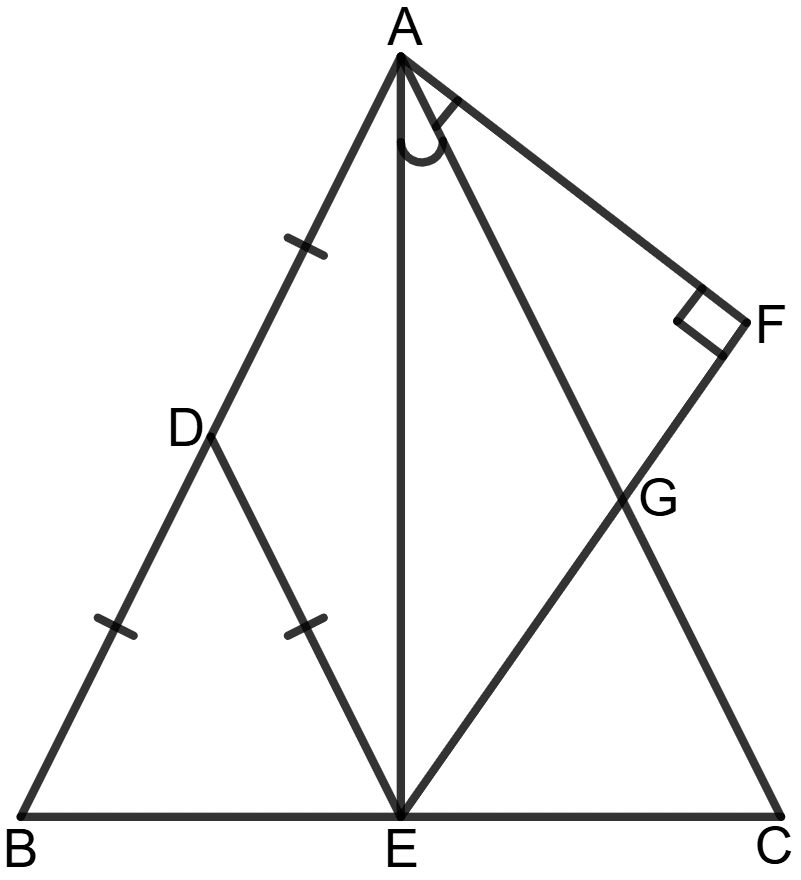
Prove that :
(i) ∠AEB = 90°
(ii) △ CEG is isosceles
(iii) ∠CEG = ∠EAF.
ABC is an equilateral triangle. If AD bisects angle A, prove that AD is perpendicular bisector of BC.
In the following figure, AE//BC. Find values of x and y.