Mathematics
Which of the following pairs of triangles are congruent ?
(a) △ABC and △DEF in which : BC = EF, AC = DF and ∠C = ∠F.
(b) △ABC and △PQR in which : AB = PQ, BC = QR and ∠C = ∠R.
(c) △ABC and △LMN in which : ∠A = ∠L = 90°, AB = LM, ∠C = 40° and ∠M = 50°
(d) △ABC and △DEF in which : ∠B = ∠E = 90°, AC = DF
Answer
(a) In △ABC and △DEF,
⇒ BC = EF [Given]
⇒ AC = DF [Given]
⇒ ∠C = ∠F [Given]
∴ △ABC ≅ △DEF (By S.A.S axiom)
Hence, △ABC and △DEF are congruent by S.A.S axiom.
(b) Given,
In △ABC and △PQR,
⇒ AB = PQ [Given]
⇒ BC = QR [Given]
⇒ ∠C = ∠R [Given]
Here the equal angles are not the included angles, thus the triangles are not necessarily congruent.
Hence, △ABC and △PQR are not necessarily congruent.
(c) Given,
In △ABC,
⇒ ∠A + ∠B + ∠C = 180°
⇒ 90° + ∠B + 40° = 180°
⇒ ∠B + 130° = 180°
⇒ ∠B = 180° - 130°
⇒ ∠B = 50°.
In △ABC and △LMN,
⇒ AB = LM [Given]
⇒ ∠B = ∠M [Both equal to 50°]
⇒ ∠A = ∠L [Both equal to 90°]
∴ △ABC ≅ △LMN (By A.S.A axiom)
Hence, △ABC and △LMN are congruent by A.S.A axiom.
(d) Given,
In △ABC and △DEF,
⇒ ∠B = ∠E = 90°
⇒ AC = DF
⇒ AB = DE
∴ △ABC ≅ △DEF (By R.H.S. axiom)
Hence, △ABC and △DEF are congruent by R.H.S. axiom.
Related Questions
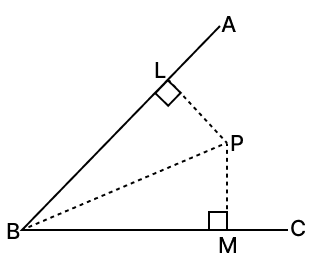
In the given figure, P is a point in the interior of ∠ABC. If PL ⊥ BA and PM ⊥ BC such that PL = PM, prove that BP is the bisector of ∠ABC.
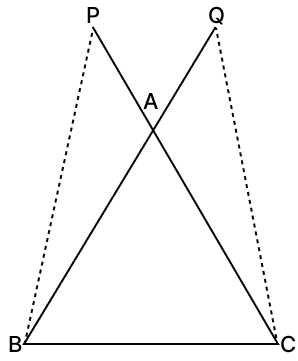
In the given figure, equal sides BA and CA of △ABC are produced to Q and P respectively such that AP = AQ. Prove that PB = QC.
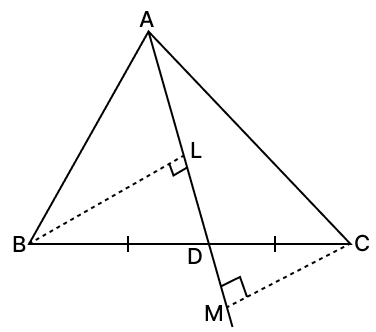
In the given figure, median AD of △ABC is produced. If BL and CM are perpendiculars drawn on AD and AD produced, prove that BL = CM.
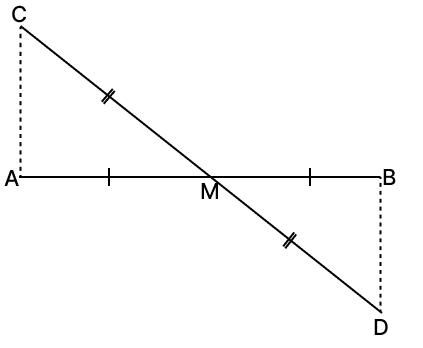
In the given figure, M is the mid-point of AB and CD. Prove that CA = BD and CA || BD.