Mathematics
Four identical cubes are joined end to end to form a cuboid. If the total surface area of the resulting cuboid is 648 cm2; find the length of edge of each cube.
Also, find the ratio between the surface area of the resulting cuboid and the surface area of a cube.
Mensuration
7 Likes
Answer
Given:
Total surface area of the cuboid = 648 cm2
Let a be the side of each cube.
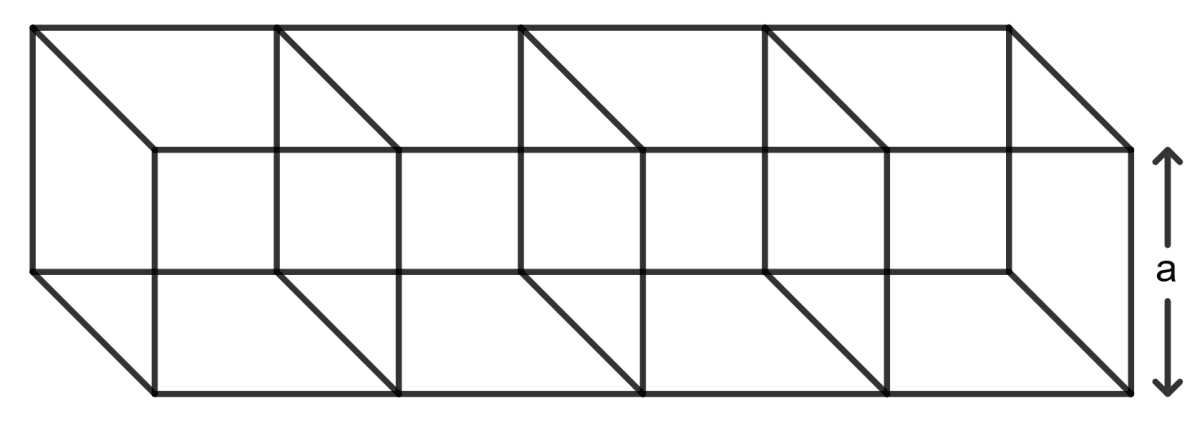
When four identical cubes are placed adjacently, the cuboid's dimensions are:
Length = a + a + a + a = 4a
Breadth = a
Height = a
Total surface area of the cuboid = 2(lb + bh + hl)
⇒ 2(4a x a + a x a + a x 4a) = 648
⇒ 2(4a2 + a2 + 4a2) = 648
⇒ 2 x 9a2 = 648
⇒ 18a2 = 648
⇒ a2 =
⇒ a2 = 36
⇒ a =
⇒ a = 6
Thus, the length of the edge of each cube is 6 cm.
Hence, the edge of each cube is 6 cm, and the ratio of the surface area of the resulting cuboid to that of one cube is 3:1.
Answered By
1 Like
Related Questions
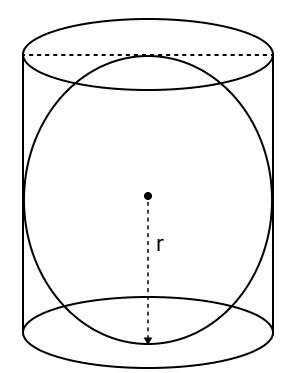
Assertion (A): A sphere is inscribed in a cylinder the ratio of the volume of the cylinder to the volume of the sphere is 1 : 4.
Reason (R): Required ratio = πr2 x 2r : πr3
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
A hollow square-shaped tube open at both ends is made of iron. The internal square is of 5 cm side and the length of the tube is 8 cm. There are 192 cm3 of iron in this tube. Find its thickness.
A rectangular card-board sheet has length 32 cm and breadth 26 cm. Squares each of side 3 cm, are cut from the corners of the sheet and the sides are folded to make a rectangular container. Find the capacity of the container formed.
A swimming pool is 18 m long and 8 m wide. Its deep and shallow ends are 2 m and 1.2 m respectively. Find the capacity of the pool, assuming that the bottom of the pool slopes uniformly.