Mathematics
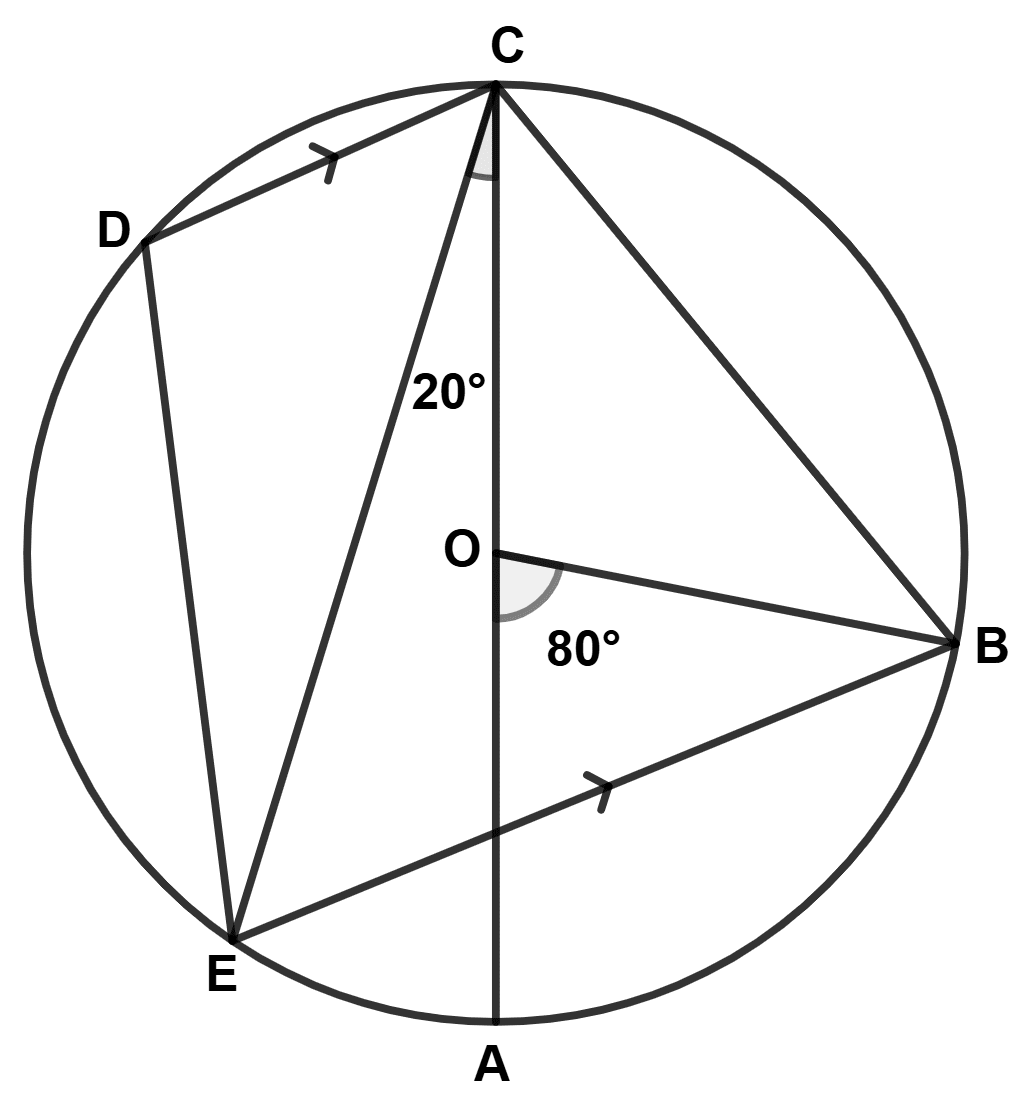
In the given figure AC is the diameter of the circle with center O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°. Calculate :
(a) ∠BEC
(b) ∠BCD
(c) ∠CED
Circles
ICSE Sp 2025
80 Likes
Answer
(a) Join AE.
We know that,
The angle subtended by a chord at the centre is twice the angle subtended on the circumference.
∴ ∠AOB = 2∠AEB
⇒ 80° = 2∠AEB
⇒ ∠AEB = = 40°.
We know that,
Angle in a semi-circle is a right angle.
⇒ ∠AEC = 90°
From figure,
⇒ ∠BEC = ∠AEC - ∠AEB = 90° - 40° = 50°.
Hence, ∠BEC = 50°.
(b) From figure,
⇒ ∠ECD = ∠CEB = 50° (Alternate angles are equal)
We know that,
The angle subtended by a chord at the centre is twice the angle subtended on the circumference.
⇒ ∠AOB = 2∠BCA
⇒ 80° = 2∠BCA
⇒ ∠BCA = = 40°.
From figure,
⇒ ∠BCD = ∠BCA + ∠ACE + ∠ECD = 40° + 20° + 50° = 110°.
Hence, ∠BCD = 110°.
(c) As sum of opposite angles of cyclic quadrilateral = 180°.
⇒ ∠BED + ∠BCD = 180°
⇒ ∠BED = 180° - ∠BCD = 180° - 110° = 70°.
From figure,
⇒ ∠BED = ∠BEC + ∠CED
⇒ 70° = 50° + ∠CED
⇒ ∠CED = 70° - 50° = 20°.
Hence, ∠CED = 20°.
Answered By
50 Likes
Related Questions
While factorizing a given polynomial, using remainder and factor theorem, a student finds that (2x + 1) is a factor of 2x3 + 7x2 + 2x - 3.
(a) Is the student's solution correct stating that (2x + 1) is a factor of the given polynomial ? Given a valid reason for your answer.
(b) Factorize the given polynomial completely.
A line segment joining P (2, -3) and Q (0, -1) is cut by the x-axis at the point R. A line AB cuts the y-axis at T(0, 6) and is perpendicular to PQ at S. Find the :
(a) equation of line PQ
(b) equation of line AB
(c) coordinates of points R and S.
In a Geometric Progression (G.P.) the first term is 24 and the fifth term is 8. Find the ninth term of the G.P.
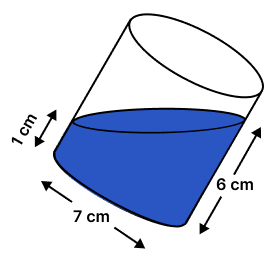
In the adjoining diagram, a tilted right circular cylindrical vessel with base diameter 7 cm contains a liquid. When placed vertically, the height of the liquid in the vessel is the mean of two heights shown in the diagram. Find the area of wet surface, when the cylinder is placed vertically on a horizontal surface. (Use )