Mathematics
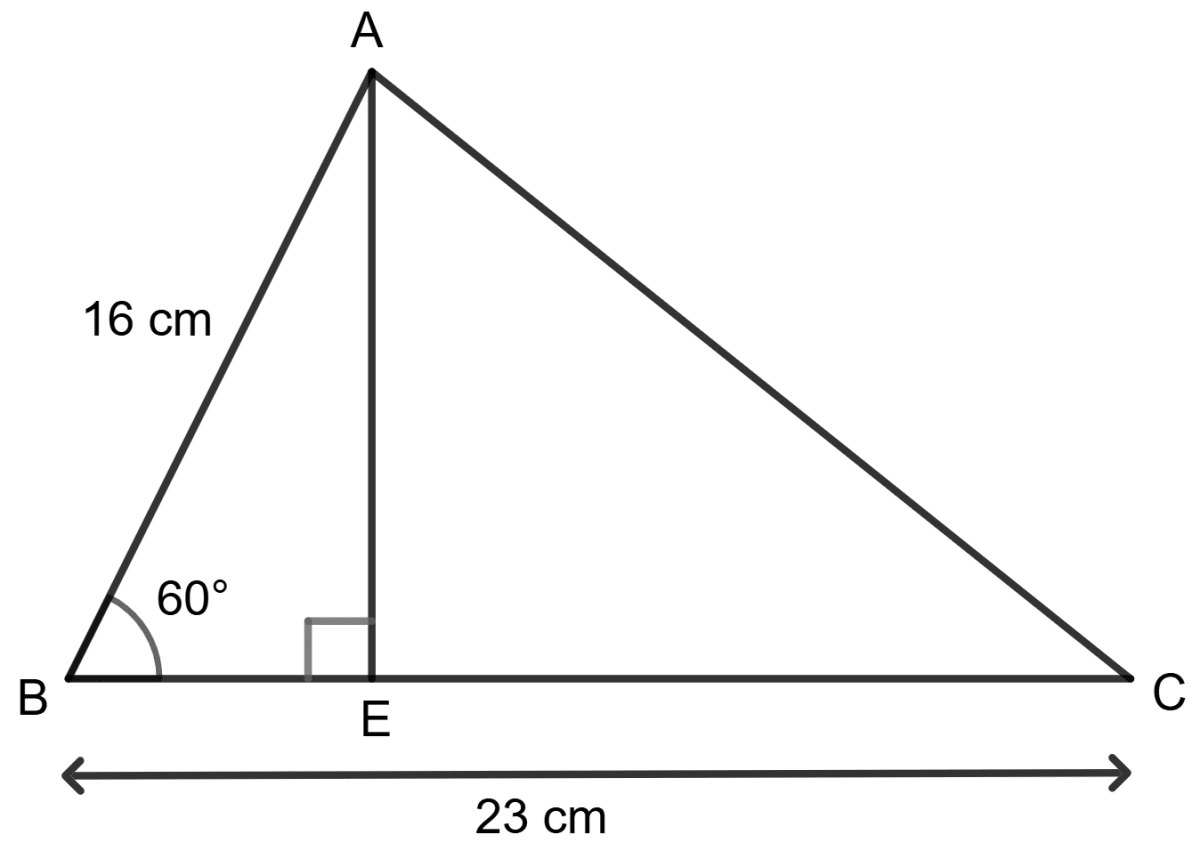
In the given figure, ∠B = 60°, AB = 16 cm and BC = 23 cm. Calculate :
(i) BE
(ii) AC.
Trigonometric Identities
11 Likes
Answer
(i) In Δ ABE,
Hence, BE = 8 cm.
(ii) In Δ ABE, according to Pythagoras theorem,
⇒ AB2 = BE2 + EA2 (∵ AB is hypotenuse)
⇒ 162 = 82 + EA2
⇒ 256 = 64 + EA2
⇒ EA2 = 256 - 64
⇒ EA2 = 192
⇒ EA =
⇒ EA = 8
EC = BC - BE
= 23 - 8 cm
= 15 cm
In Δ AEC, according to Pythagoras theorem,
⇒ AC2 = AE2 + EC2 (∵ AC is hypotenuse)
⇒ AC2 = (8 )2 + 152
⇒ AC2 = 192 + 225
⇒ AC2 = 417
⇒ AC = = 20.42 cm
Hence, AC = 20.42 cm.
Answered By
7 Likes
Related Questions
Find the length of AB.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
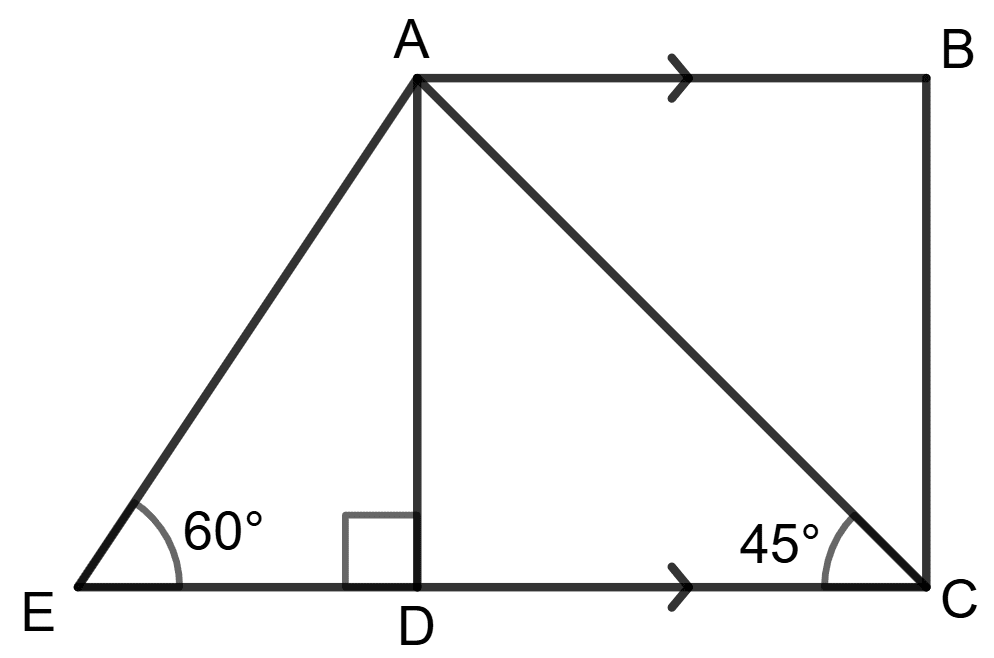
Given that ∠AED = 60° and ∠ACD = 45°; calculate :
(i) AB
(ii) AC
(iii) AE
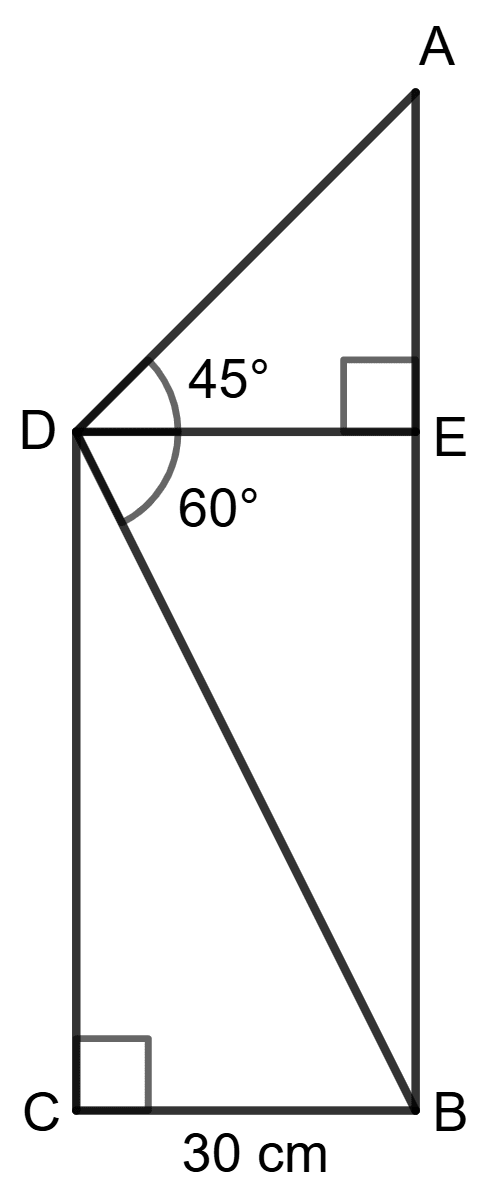
Find :
(i) BC
(ii) AD
(iii) AC

In right-angled triangle ABC; ∠B = 90°. Find the magnitude of angle A, if :
(i) AB is times of BC.
(ii) BC is times of AB.