Mathematics
In the given figure (drawn not to scale) chords AD and BC intersect at P, where AB = 9 cm, PB = 3 cm and PD = 2 cm.
(a) Prove that △ APB ~ △ CPD
(b) Find the length of CD
(c) Find area △ APB : area △ CPD.
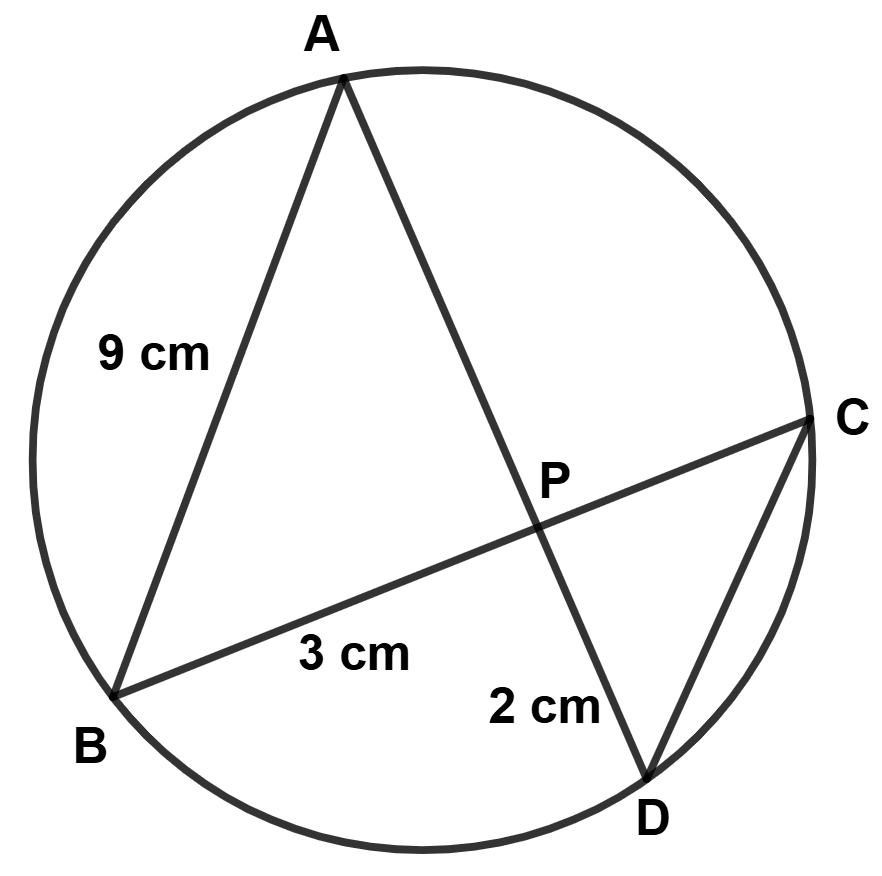
Circles
ICSE Sp 2025
43 Likes
Answer
(a) In △ APB and △ CPD,
⇒ ∠APB = ∠CPD (Vertically opposite angles are equal)
⇒ ∠BAP = ∠DCP (Angles in same segment are equal)
∴ △ APB ~ △ CPD (By A.A. axiom)
Hence, proved that △ APB ~ △ CPD.
(b) We know that,
Corresponding sides of similar triangles are proportional.
Hence, CD = 6 cm.
(c) We know that,
Ratio of area of similar triangles is equal to the ratio of square of the corresponding sides.
Hence, area △ APB : area △ CPD = 9 : 4.
Answered By
23 Likes
Related Questions
Solve the following inequation, write the solution set and represent it on the real number line.
5x - 21 < , x ∈ R.
Prove the following trigonometry identity :
(sin θ + cos θ)(cosec θ - sec θ) = cosec θ.sec θ - 2 tan θ
Mr. Sameer has a recurring deposit account and deposits ₹ 600 per month for 2 years. If he gets ₹ 15600 at the time of maturity, find the rate of interest earned by him.
Using step-deviation method, find mean for the following frequency distribution
Class Frequency 0-15 3 15-30 4 30-45 7 45-60 6 60-75 8 75-90 2