Mathematics
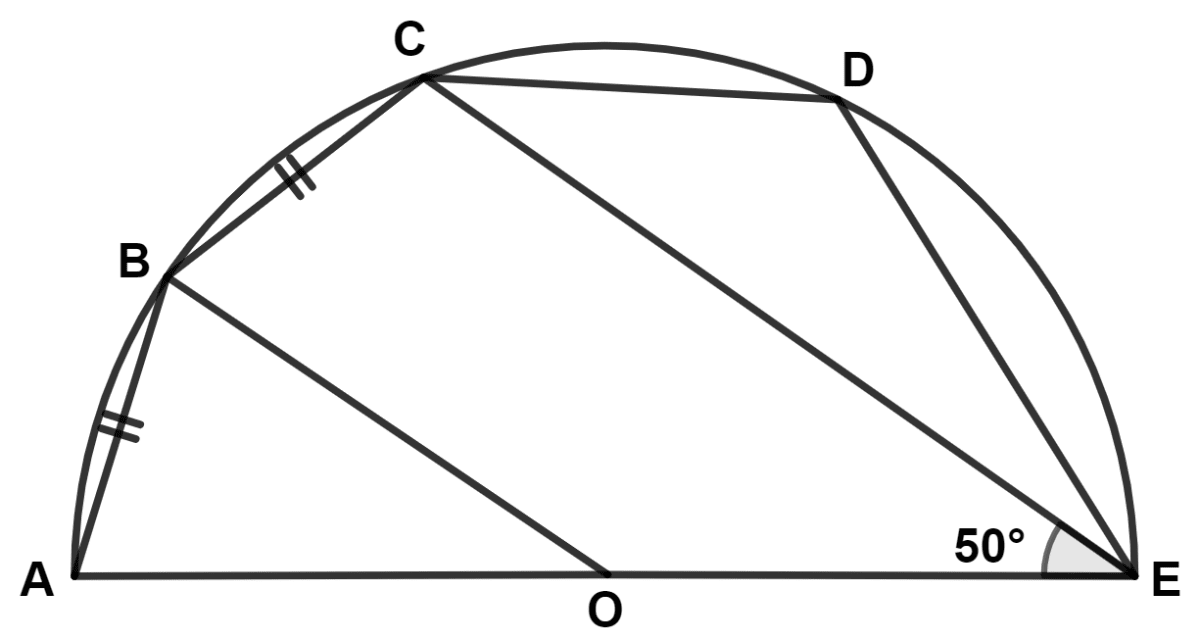
The given figure shows a semicircle with center at point O and AE as diameter. Chord AB = chord BC and angle CEO = 50°.
(i) Find angle AOB.
(ii) Show that OB is parallel to EC.
Circles
21 Likes
Answer
(i) From figure,
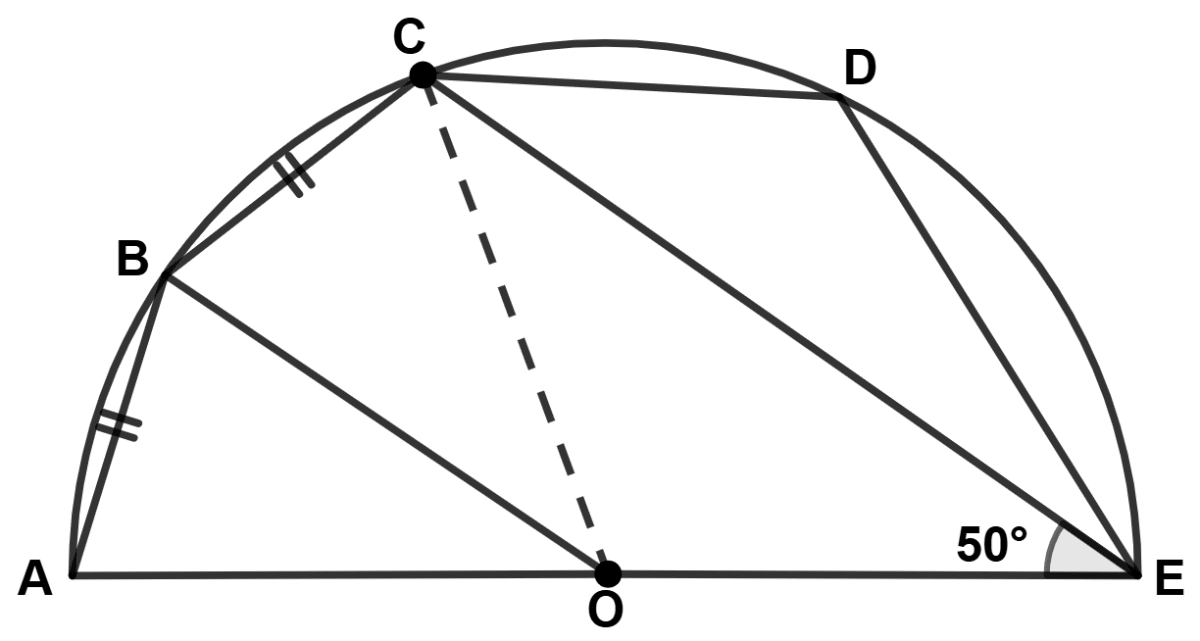
⇒ OE = OC (Radius of same circle)
⇒ ∠OCE = ∠OEC = 50° (Angles opposite to equal sides are equal)
In △ OEC,
⇒ ∠COE + ∠OCE + ∠OEC = 180° (Angle sum property of triangle)
⇒ ∠COE + 50° + 50° = 180°
⇒ ∠COE + 100° = 180°
⇒ ∠COE = 180° - 100° = 80°.
We know that,
Equal chords subtend equal angles at the center.
∴ ∠AOB = ∠BOC = x (let)
From figure,
⇒ ∠AOB + ∠BOC + ∠COE = 180° [∵ AE is a straight line]
⇒ x + x + 80° = 180°
⇒ 2x = 180° - 80°
⇒ 2x = 100°
⇒ x = = 50°.
Hence, ∠AOB = 50°.
(ii) ∠BOC = x = 50°.
Since,
⇒ ∠BOC = ∠OCE = 50°
From figure,
∠BOC and ∠OCE are alternate angles and are equal.
∴ OB || CE.
Hence, proved that OB || CE.
Answered By
15 Likes
Related Questions
(i) Evaluate :
(ii) Evaluate :
(iii) Prove that : = 2.
If a, b and c are in continued proportion, prove that :
abc(a + b + c)3 = (ab + bc + ca)3.
Use a graph for this question. Draw an ogive for the given distribution. From the graph determine :
(i) the median
Marks No. of students 0-10 5 10-20 10 20-30 14 30-40 21 40-50 25 50-60 34 60-70 36 70-80 27 80-90 16 90-100 12 (ii) the number of students scoring above 65 marks.
(iii) if 10 students qualify for merit scholarship, find the minimum marks required to qualify.
(iv) the number of students who did not pass, if the pass percentage was 35.
If matrix A = and I is a unit matrix of order 2; find the value of m so that :
A2 - 2A - mI = 0