Mathematics
The given figure shows two congruent circles with centres P and Q. R is mid-point of PQ and ABRCD is a straight line.
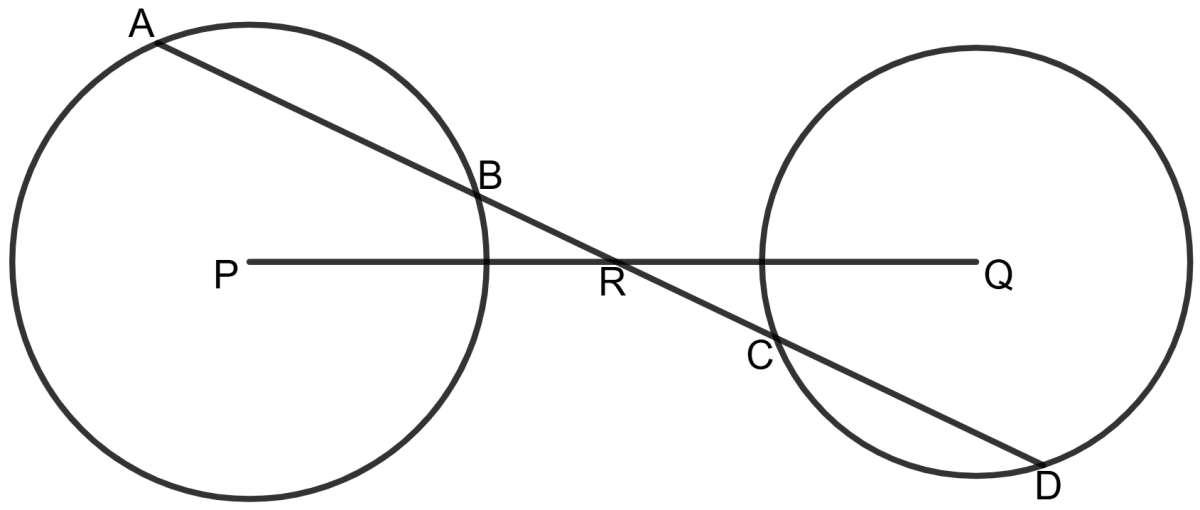
Prove that : AB = CD.
Circles
4 Likes
Answer
Given: Two congruent circles with centres P and Q. Point R is the midpoint of PQ and ABRCD is a straight line.
To proof: AB = CD
Construction: Draw PM ⊥ AB and QO ⊥ CD.
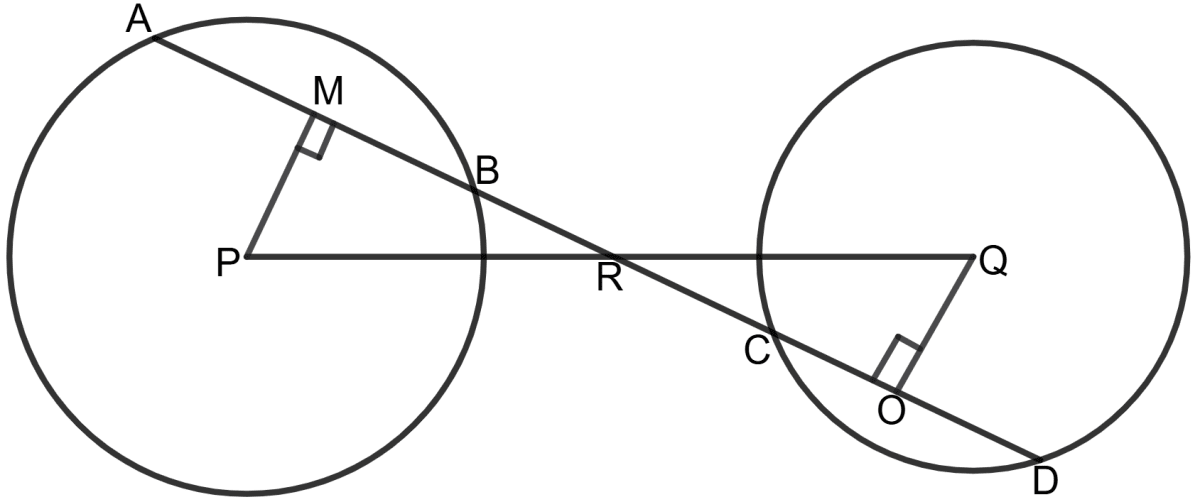
Proof: In triangles Δ MPR and Δ OQR:
∠MRP = ∠ORQ (Vertically opposite angles)
∠PMR = ∠QOR = 90° (Since PM ⊥ AB and QO ⊥ CD)
RP = RQ (Since R is the midpoint of PQ)
So, by ASA congruency criterion:
Δ MPR ≅ Δ OQR
By corresponding parts of congruent triangles,
⇒ PM = QO
Now, in congruent circles, if the perpendicular distances of two chords from the centres are equal, then the chords are also equal.
⇒ AB = CD
Hence, AB = CD.
Answered By
1 Like
Related Questions
Two circles of radii 10 cm and 17 cm intersecting each other at two points and the distance between their centres is 21 cm. Find the length of the common chord.
In the given circle, arc APB and arc BQC are in the ratio 2 : 5 and O is centre of the circle.
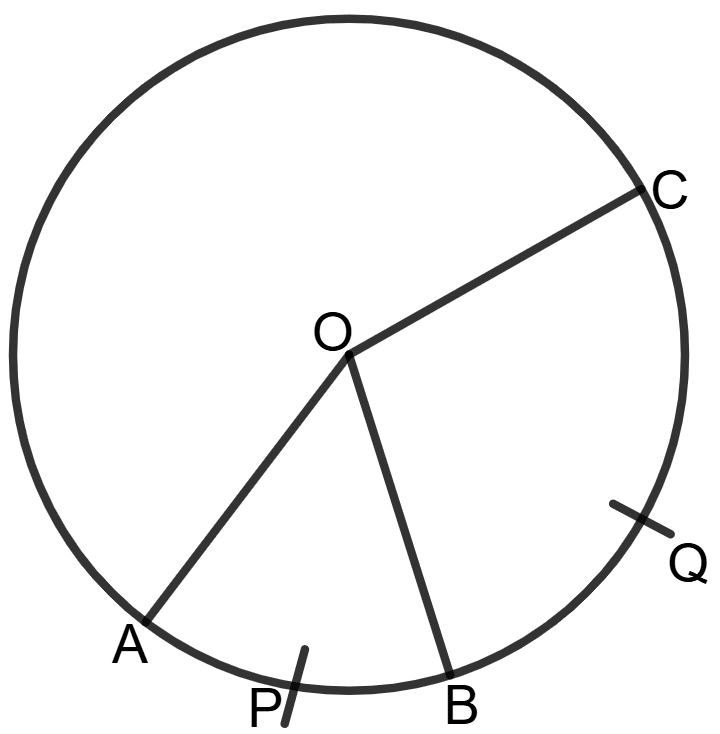
If angle AOB = 44°; find angle AOC.
In the given figure, O is the centre of the given circle. AB is a side of a square, BC is a side of regular pentagon and CD is a side of regular hexagon. Find :
(i) ∠AOB
(ii) ∠AOC
(iii) ∠AOD
(iv) ∠BCD
Construct a cumulative frequency distribution table from the following frequency table :
C.I. Frequency 0-12 12 12-24 16 24-36 15 36-48 10 48-60 18